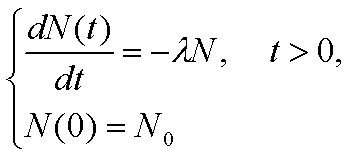 (P)
(P)今日は、次の簡単な常微分方程式を用いて授業を進めます。この方程式は、例えば放射性同位体の崩壊を記述するモデル方程式として導出されます。例えば放射性炭素による年代測定にはこういった微分方程式が役立ちます。N(t) を時刻 t における放射性同位体の原子数とすると下記のような微分方程式が得られます。(詳しい説明は来週やります。)
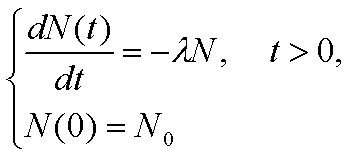 (P)
(P)
さて、この微分方程式は簡単に解けて、解は次のようになります。
N(t) = N0 e-λt (S)
最初の目標は、解(S)をグラフとして表示するプログラムを作成することです。パラメータλおよびN0を与えれば、(S)のグラフをかけるはずです。コンピュータを用いてこのようなグラフを描く場合には折れ線近似で描く必要があります。
課題0
1階常微分方程式の初期値問題(P)を解け。
Python でグラフを描くために、matplotlibを用います(マニュアル)。また、数学関数を用いるので、mathモジュールも利用します。その為、Pythonコードのはじめに、以下のコードが必要となります。情報処理の復習すべき箇所はここ。
import math import matplotlib.pyplot as plt
課題1(演習)
matplotlibを用いて、
N(t) = N0 e-λt (S)
のグラフを描け。ただし、
N0=1, λ=1, 0≦t≦10
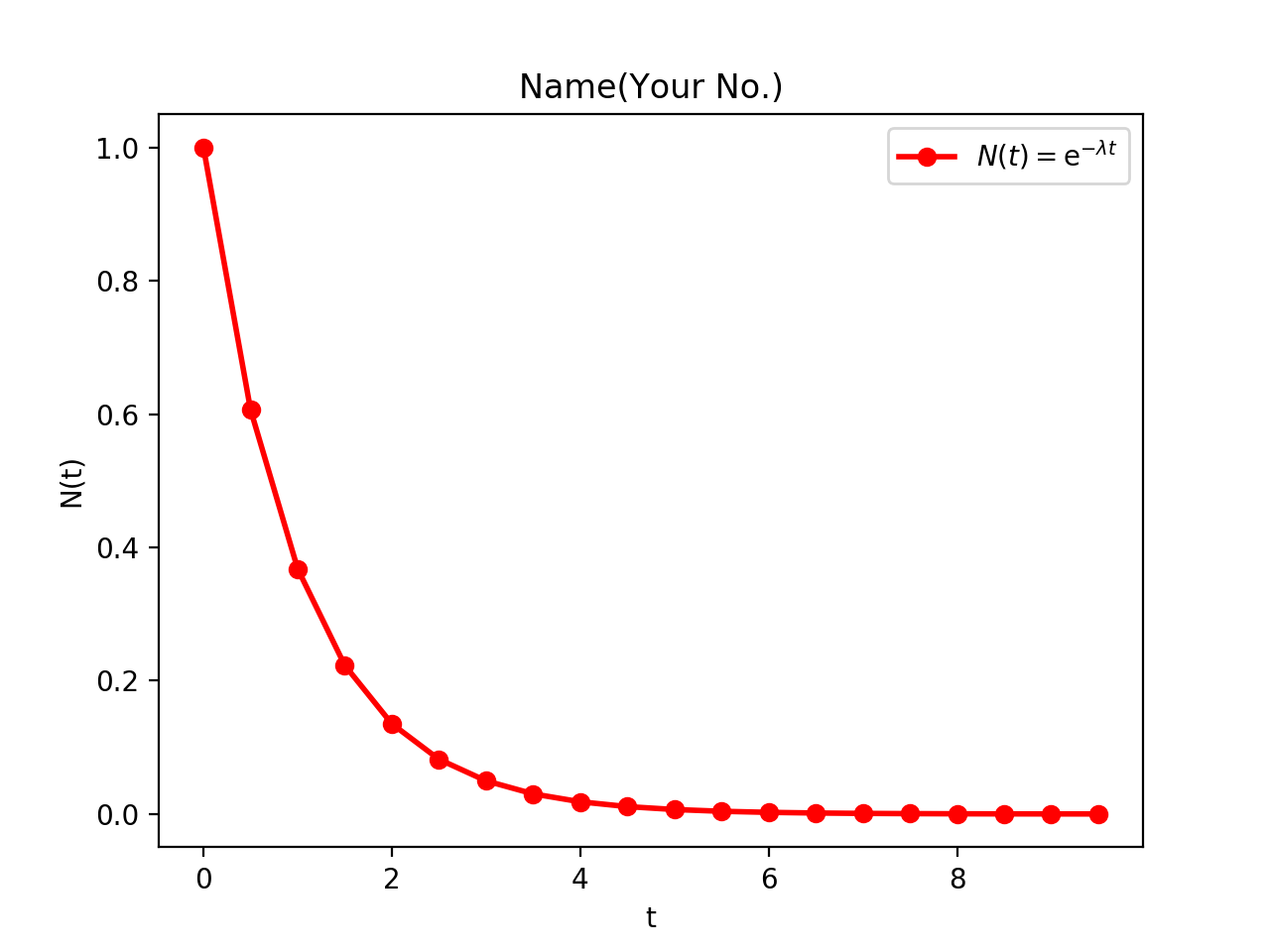
とする。例えば次のようになる。(この例では、0≦t≦10 を 20等分している。つまり時間刻み幅を dt と書くことにすると、 dt = 10.0/20.0 = 0.5 である。曲線を20本の直線のつながりである折れ線で近似するのである。)
Pythonのmathモジュールでは,ea は math.exp(a) で求まる。
課題2
N0=1, λ=1のとき,N(τ) = 0.5 となる τ を求めよ。((S)を用いて具体的に求めよ)
答え: log2 (約 0.693)
Pythonのmathモジュールでは log2 は math. log(2.0) で求まる。
次の課題で作成するプログラムでは、N(t)を関数として定義すると綺麗なプログラムになる(使わなくても作成できる)。Pythonにおける関数の定義等の説明は、数理工学実験2のここを参照。授業中に少し解説する。
課題3(演習)(次回レポート課題となる予定)
課題1で作成したプログラムを用いて課題2のτを近似的に次のような手法で求めたい。そのようなプログラムを作成せよ。
方法
N(t) の値を(S)を用いて飛び飛びの t の値 ti = dt*i (ただし dt は時間刻み幅)について求めるのであるが、(S)と課題1のグラフから明らかなように N(t) は単調減少関数である。であるから、
N(ti) ≧ 0.5 >N(ti+1)
となる i がただ一つあるであろう。このとき、 ti を τ の近似値 τ* とする。
小問1:τ* を求めよ.
小問2:
0≦t≦10 を 100等分して上記方法にてτ* を求め、課題2で求めた値との差(誤差と呼ぶ)
err* = |τ- τ*|
を求めよ。
注意:当然ながら刻み数を 100 から 1000 に増やせばより正確な値が求まる。
小問3:
err* は刻み数を変更するとどのようにかわるか?刻み数100, 1000,10000に関してそれぞれ調べ,横軸を刻み数,縦軸をその刻み数に対するerr* として,グラフにしてみよ(例えばExcelを用いる).
課題4(次回レポート課題となる予定)
課題3の方法ではあまり良い精度で近似値を求めることができない。次の方法でより精度良く近似値をもとめることを考える。課題3と同様に,
N(ti) ≧ 0.5 >N(ti+1)
なる i を求め、2点 (ti, N(ti)), (ti+1, N(ti+1)) を結ぶ直線を考える(下図の青丸および青線).その直線と N = 0.5 の直線の交点の t の値 τ** をもって、τ の近似値をする(下図赤丸).このような手法を線形補間と呼ぶ.下図において,黒い曲線がN(t)であって,黄緑色の丸がτである(ただし,N(t)はわかりやすいように強調して描いてある).
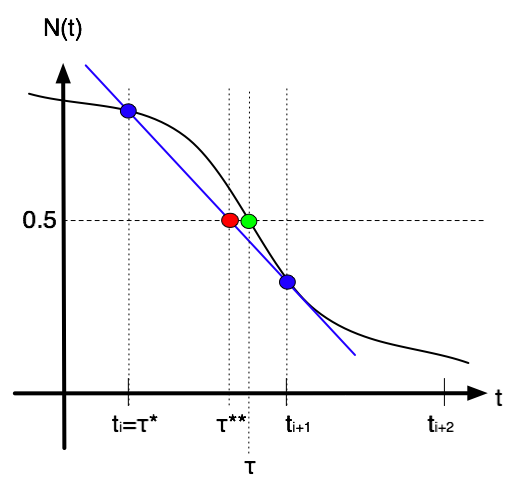
小問1:τ** を求めよ.
小問2:
0≦t≦10 を 100等分して上記方法にて τ** を求め、課題2で求めた値との差
err** = |τ- τ**|
を求めよ。課題3の結果よりも良いだろうか?
注意:
課題3の方法でも刻み数を増やせばより正確な値が求まるのであるが、課題4の補間を使えば、あまり多くない刻み数でも正確な近似値が得られることを実感してほしい。
小問3:
err**は刻み数を変更するとどのようにかわるか?刻み数100, 1000,10000に関してそれぞれ調べ,横軸を刻み数,縦軸をその刻み数に対するerr**として,グラフにしてみよ(例えばExcelを用いる).
小問4:
課題3の小問3および,課題4の小問3にて得られたグラフを重ねて表示してみよ(例えばExcel を用いる).
課題5(次回レポート課題となる予定)
課題4において刻み数100で近似値を求めた場合の誤差と同程度に小さい誤差とするためには課題3において刻み数をどの程度にしなければならないか。実験してみよ。
注意:
課題3、課題4の方法は、 N(t) が具体的に関数として与えられていない場合(例えば実測データなど)にも有効であることに注意。
課題3、課題4は2分法の離散版とみることもできます。N(t)の具体的な関数形が分かっている場合(例えば今回の場合)には、2分法やニュートン法(教科書2章)等の方法で根を求める事ができます。
今回は、微分方程式を数値的に解いたわけではないことに注意してください。解析的にもとまった解(S)をグラフにしたにすぎません。来週は、常微分方程式を数値的に解いてもらい、それをグラフ化してもらいます。
課題3,課題4の内容の発展的内容として次の問題も考えてみて下さい.
簡単な発展問題であるが,実際に取り組むことが重要である.いくつか重要な事を学ぶことができる.(例えば,課題3,4では,関数は単調減少関数であったが,これは違う為,交点部分の判定に工夫がいるであろう.)
課題3および課題4の方法を用いて,
y = sin(x*x)
と直線
y = 0.5
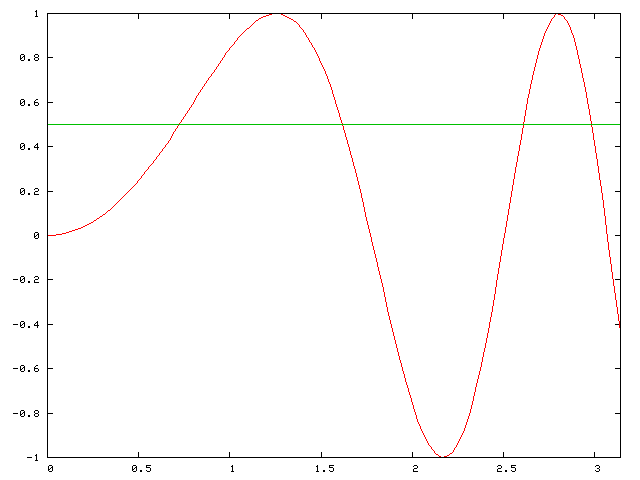
の交点の x 座標を 0≦x≦πの範囲で全て求めよ.下のグラフに示すように(縦軸をy,横軸をx とした),交点は4つ存在する.
課題1で作成したグラフとそれを作成したPythonコードをWordファイルに貼り付け、それをPDF形式で保存したものを提出してください。詳しくは授業中に指示しますのでそれに従ってください。次回以降のレポートと提出課題については同様のルールとします。
課題1の例にあるように、軸名と凡例およびグラフのタイトル(Name(Your No.) となっている部分を自分の名前(ローマ字)と学生番号とすること)も入れる。いれかたは、情報処理のここを参照。凡例部分の label については、
label="$N(t)=\mathrm{e}^{- \lambda t}$"
とする(TeX記法を習っていないようなので)。
(注意)