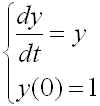
前回はオイラー法を用いた数値解法の演習を行いました．オイラー法は単純でそれはそれでよいのですが、実際の解に近い数値解を出すためには、時間刻み幅 h をかなり小さくとらねばならないことが前回の課題４によってわかります．そこで、より精度の高い解法が必要となりますが、今回はそのような解法として、ルンゲ・クッタ法を扱い、それを用いた数値解法の演習を行います．
ルンゲ・クッタ法の導出については、このページの最後を参照してください（詳細は参考書を参照してください）．ルンゲ・クッタ法は次にしめすようなアルゴリズムで、オイラー法に比べれば多少複雑なものとなっています（赤字の部分が異なります）．
T を解を求める時間の上限とし、h を時間刻み幅、N を時間刻み数とします．また、変数は y とし、a を初期値とします．r1, r2, r3, r4 はそれぞれ実数型の変数です．
T,N,h を定める
a の入力を受ける (fprintf 関数 + scanf 関数）
y = a
t = 0 での y の値の表示 (printf 関数)
i = 0,1,2,....,N-1の順に
t = i*h
r1 = f(t, y)
r2 = f(t + h/2, y + (h/2)*r1)
r3 = f(t + h/2, y + (h/2)*r2)
r4 = f(t + h, y + h*r3)
y_new = y + (h/6)*(r1 + 2*r2 + 2*r3 + r4)
y = y_new
(一定間隔毎に)t+h と y_new の表示 (printf関数)
を繰り返す
課題１
上記のルンゲ ･クッタ法を用いて、次の問題を実際に解き、ルンゲ ･クッタ法がオイラー法と比べてどの程度性能が良いか比べよ．次の初期値問題を 0≦t≦5 の範囲で h=0.5 とし、実際にオイラー法とルンゲ ･クッタ法を用いて解け．
オイラー法を用いた解法プログラムを ~/work/Part11-1.c とし、同問題をルンゲ･クッタ法を用いて解くプログラムを ~/work/Part11-2.c とする．微分解 y(t) = exp(t) とどの程度あっているか、gunuplot を用いて確認せよ．
結果は大体次のようになります．h=0.5とかなり粗く時間刻み幅をとっているにも関わらず、ルンゲ ･クッタ法は良く微分解を近似できていることがわかります．それに比べてオイラー法は微分解から大きく離れてしまっています．これでは正しい計算とは言えないでしょう．
前回の課題で扱った
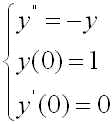（１）
をy1(t)=y(t), y2(t)=y'(t) とおいて次のように連立の１階の常微分方程式に帰着したもの
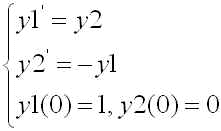（２）
を再び考えます．このような連立の常微分方程式をルンゲ ･クッタ法を用いて解く場合のアルゴリズムを次に示します．ただし、 T を解を求める時間の上限とし、h を時間刻み幅、N を時間刻み数とします．また、変数は y1, y2 とし、それぞれの初期値を a1, a2 とします．r11, r21, r31, r41, r12, r22, r32, r42 および y1_new, y2_new はそれぞれ実数型の変数です．また、f1(t, y1, y2) および f2(t, y1, y2) はそれぞれ実数型の関数で（２）式の場合には f1 が第一式の右辺、 f2 が第二式の右辺となります．
T,N,h を定める
a1, a2 の入力を受ける (fprintf 関数 + scanf 関数）
y1 = a1
y2 = a2
t = 0 での y1, y2 の表示 (printf 関数)
i = 0,1,2,....,N-1の順に
t = i*h
r11 = f1(t, y1, y2)
r12 = f2(t, y1, y2)
r21 = f1(t + h/2, y1 + (h/2)*r11, y2 + (h/2)*r12)
r22 = f2(t + h/2, y1 + (h/2)*r11, y2 + (h/2)*r12)
r31 = f1(t + h/2, y1 + (h/2)*r21, y2 + (h/2)*r22)
r32 = f2(t + h/2, y1 + (h/2)*r21, y2 + (h/2)*r22)
r41 = f1(t + h, y1 + h*r31, y2 + h*r32)
r42 = f2(t + h, y1 + h*r31, y2 + h*r32)
y1_new = y1 + (h/6)*(r11 + 2*r21 + 2*r31 + r41)
y2_new = y2 + (h/6)*(r12 + 2*r22 + 2*r32 + r42)
y1 = y1_new
y2 = y2_new
(一定間隔毎に) t+h と y1_new, y2_new を画面に表示 (printf関数)
を繰り返す
課題２
ルンゲ・クッタ法を用いて（２）を解け．前回同様、0≦t≦20の範囲において、h=0.0001,0.001, 0.01, 0.1それぞれの場合について微分解 y(t)=cos(t) とどの程度あっているか各自調べよ．
課題３
これまでは、横軸を t 、縦軸を y としたグラフを描いてもらいました．例えば横軸を y、縦軸を y' としたグラフを描いてみて下さい．どのようにすればよいでしょうか？またどのようなグラフになりますか？やってみて下さい．
課題４
重力の作用のみを受けて運動する物体を考えます（真空中でボールを投げるような状況）．ニュートンの運動の第二法則から物体の時刻 t での鉛直方向の位置を y(t) とするとその物体の鉛直方向での運動は次のような常微分方程式で表されます．（下向きを正とする）
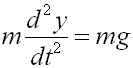（５）
m は物体の質量、g は重力加速度です．色々な初期値 y(0), y'(0) を与えてシミュレーションしてみて下さい．
課題５
さらに、上の問題に空気の抵抗のようなものを加味してみましょう．物体にかかる抵抗がそのときの物体の速度に比例するとすると、運動方程式は、
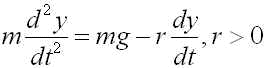（６）
となります．ただし、r は抵抗の強さを表します．色々な初期値および m, r で計算してみてください．空気抵抗を加味する前と様子は変わりましたか？
なお、両問題とも解析的に解ける問題ですので、実際に解いてみて、今回のシミュレーション結果と見比べて理解を深めて下さい．
課題６
上の両問題では物体の鉛直方向のみの運動を考えましたが、水平方向の運動も加味するとどのような運動方程式になり、その解はどのようになりますか？運動方程式を立て、シミュレーションしてみて下さい．
課題７
惑星の運動を考えます．万有引力の法則から２物体（質量はそれぞれ M,m）に働く力は
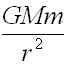
となります．rは２物体間の距離、Gは万有引力定数で
です．原点に太陽（質量 M）があり、惑星（質量 m）の位置を
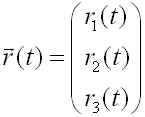
とします．惑星に働く力は
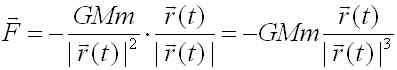
となり、
より
とおくと、２階の常微分方程式の初期値問題
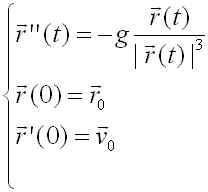
が得られます．これを１階の常微分方程式系に直し、数値計算にて解をもとめて下さい．
課題８
１９６０年代初頭に気象学者エドワード・ローレンツは流体力学に基づく次のような単純な３変数系の常微分方程式を示しました．
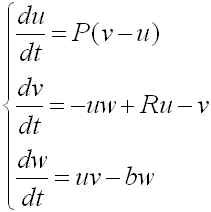
このモデルはいわゆるカオスを生じるモデルとして有名です．パラメータは P, R, b の３種類がありますが、P=16, b = 4, R=35として、u-w平面に解の軌道をプロットすると次のような図ができあがります．（初期値 (u0, v0, w0) = (5, 5, 5), t=0 から t=100 までの計算結果を線でつないだもの）
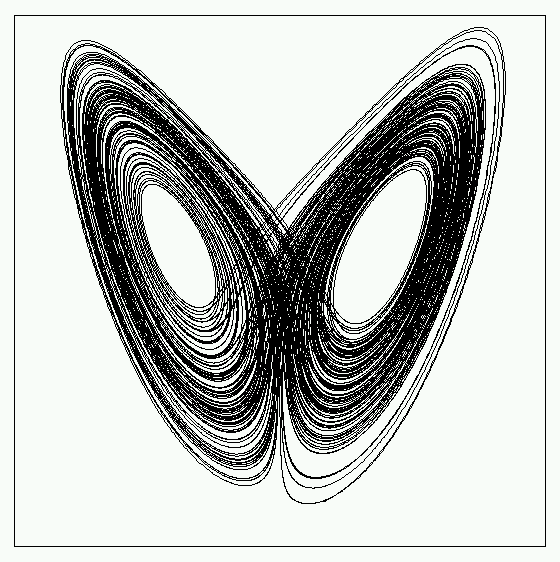
これはストレンジアトラクター（奇妙なアトラクター）と呼ばれるもので、有名なので目にしたことがある人も多いと思います．このようなカオス的な解の挙動が天気予報があたらない理由となっているともいわれています．例えば P=16, b=4 として R を色々と変えてみると、解の挙動があれこれ変わります．色々と試してみると面白いでしょう．
ルンゲ・クッタ法について
簡単にルンゲ ･クッタ法について説明します．演習で取り扱ったルンゲ ･クッタ法は４段公式とよばれるものですが、ここでは簡単の為、２段公式を取り扱います．
次の常微分方程式の初期値問題の数値解を求めたいとしましょう．
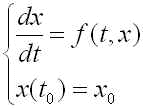（R1）
２段公式とは、 
で（R1）の近似解
が求められたとして、時間ステップ幅 h だけ進んだ 
における値 
を次の形で計算する公式です．
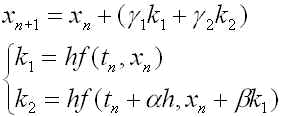（R2）
つまり、からへ進む１ステップにおいて方程式（R1）の第一式の右辺の
を２回計算するので、２段公式と呼びます．この２段公式には、パラメータ 
が含まれますが、これらは方程式（R1）の真の解 x(t)
のテイラー展開
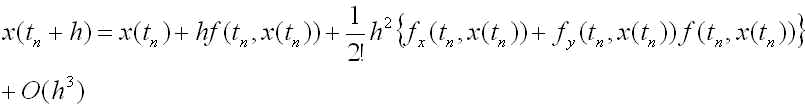（R3）
と（R2）式の第一式の同様の展開とが h のなるべく高い次数の項まで一致するように定めます．つまり、
と仮定して（R2）式の
の式の右辺を
周りでテイラー展開すると、
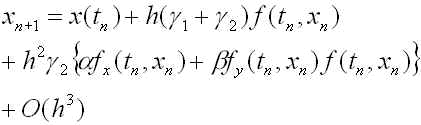（R4）
となります．これと（R3）が
の項まで一致するように
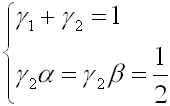（R5）
とおく．公式（R2）で定められる近似解のテイラー展開が h の２次の項まで真の解のテイラー展開に一致するという意味で、この公式を２次の公式と呼びます．この公式は２段公式でもあるので、２段２次の公式とも呼ばれます．パラメータを定める方程式（R5）には自由度が２残っているのでその定め方によって色々な公式が導かれます．（改良オイラー法、ホイン法、修正オイラー法など）
演習で用いた４段４次のルンゲ ･クッタ法の公式も同様にして求めることが出来ます．