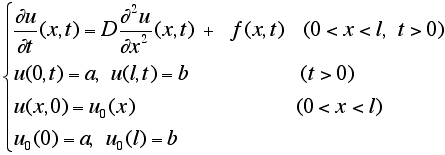
1次元拡散方程式(1次元熱伝導方程式とも呼ばれる)の初期値境界値問題とは,次のようなものです.
問題 0.1
この問題の近似解を数値計算にて求めるのが今回の目標です.まずは,上問題の特別な場合として次の問題を考えましょう.なお,式中の D は拡散係数または熱伝導率とよばれます.
問題 0.1.1
問題 0.1.1について,実際の物理現象としてどのようなものを考えているのかを簡単に説明しましょう.問題 0.1.1でみる方程式は,拡散方程式とも熱伝導方程式とも呼ばれます.拡散とは物が散らばっていく様子,例えばコップ中にインクをたらすとそれは時間とともに散らばり最終的には一様な状態になるでしょう.熱伝導とは熱が伝わる様子,例えばスプーンの端を炎で熱すると,熱は徐々に伝わり持っている部分も暑くなり火傷することになります.そういった異なる現象が同じ方程式で表現されるという面白さがあることに注意してください(方程式を導出する際の物理法則が違うが,それらが式として表現した場合に同じである事による).ここでは,問題 0.1.1を熱伝導方程式,つまり,熱の伝わる様子を表現する方程式としてみることにします.(ここでの境界条件などが,熱伝導方程式としてみたほうが自然である為.)
ここでは,大変細い棒のようなものの温度分布が時間とともにどのように変化するかといった問題をイメージでしてください.いま,棒の長さは 1 であって,時刻 t における棒の温度分布が関数 u(x,t) で与えられます.問題 0.1.1の第2行目は境界条件と呼ばれ,棒の端の状況を示しています.ここでは,すべての時刻において,端の温度は 0 であるとしてあります.状況としては,棒の両端を氷で冷やしている,つまり,両端からどんどん熱が奪われていっている状況です.ここで注意が必要なのは,実際の棒では,棒の側面からも熱が奪われるでしょうが,この問題 0.1.1の表現では,それは考えられていません.つまり,棒の側面からは熱が逃げないような状況で,端からのみ熱が逃げる状況を表現しています.もちろん,側面からの熱の収支(棒の側面を炎などで暖める状況など)も考えることができ,その場合の方程式は問題 0.1のようになります(関数 f(x,t) が熱の収支部分を表現する).問題 0.1.1の第4式は,初期条件と呼ばれ,観察をはじめる場合のはじめの時間の棒の温度分布を与えます.はじめの状態が決まらないと,その後の状態は決まらないであろうことは直感的にわかるでしょう.はじめの状態をひとつ決めた場合にその後の状態がただひとつ決まるかどうかは数学として重要な問題です.熱方程式について,そのような性質があるかどうか調べてみるとよいでしょう(解の一意性).
さて,波動方程式に対して行ったのと同様に計算機で扱えるよう離散化し,数値的に近似解を求めます.ここでは,問題0.1.1を例にすすめますが,問題0.1に対しても同様に離散化できます.
h, τはそれぞれ x, t に関する格子点の間隔で,h = 1/Nとします.また,xj = (j - 1/2)h, tk = kτ とします.さらに,
![]()
と書く事にしましょう.
波動方程式と同様にして,
(1)
は次の差分方程式で近似されます.
これを書き換えれば,
(2)
が得られます.ただし,α = Dτ/h2 としました.この式は見てのとおり,時刻 tk での u から次の時刻 tk+1 での u の値が計算できる形をしています.ようは,これをプログラムにすればよいわけです.後は,初期条件と境界条件ですが,それらはそれぞれ次のようになります.
(3)
(4)
これで,準備はできました.
次に拡散方程式を計算機にて解くためのアルゴリズムを考えましょう.解を求める時刻の上限を T とし,適当な自然数 M を定めて,τ=T/M とします.問題0.1.1を解くアルゴリズムは次のようになります(ただし D=1.0 とした).
(1)初期パラメータ設定
N, M, T, D を設定する
h := 1/N, τ:=T/M, α:= Dτ/h2
(2) 初期値設定
j := 1,....,N の順に
uj := 2xj(1-xj)
を繰り返す
u0 := -u1, uN+1 = -uN (境界条件)
(3)
k := 0,1,.....,M-1 の順に
j := 1,2,....,N の順に
new_uj := αuj-1 + (1 - 2α)uj + αuj+1
を繰り返す
j := 1,2,....,N の順に
uj := new_uj
を繰り返す
u0 := -u1, uN+1 = -uN (境界条件)
を繰り返す
計算結果をアニメーションとして表示する為に,GLSCの関数が途中に必要となりますが,ここでは省略しています.このアルゴリズムを実現するC のプログラムを作成せよというのが当面の課題となります.大体のあらすじを C言語 っぽく示しておきます(ほとんど完成していますが).残念ながら,このままでは初期値のまま動きませんので各自修正してください.u, new_u という2つの1次元配列を用意しています.メインの部分(実際の計算部分)はアルゴリズムを参考にして自分で考えてください.
/* 1次元拡散方程式のアニメーション */
/* 未完成版 */
#include <glsc.h>
#include <math.h>
#include <stdio.h>
/* 空間刻数 */
#define N (50)
/* 時間刻数 */
#define M (5000)
/* 時間上限 */
#define T (0.5)
/* L (棒の長さ・領域長)*/
#define L (1.0)
/* D (拡散係数) */
#define D (1.0)
/* 画面表示間隔 */
#define INTV (10)
main()
{
/* プログラム中で使用する変数の型宣言 */
int j, k;
double u[N+2], new_u[N+2], t, x, tau, h, a;
/* dt, dx 等を設定 */
tau = T/M;
h = L/N;
a = D*tau/(h*h);
/* GLSCの初期設定 */
g_init("Graph", 200.0, 100.0);
g_device(G_DISP);
/* 仮想座標系を一つ用意 */
g_def_scale(0, 0.0, L, 0.0, 1.0, 10.0, 10.0, 180.0, 80.0);
g_cls();
g_sel_scale(0);
/* 初期値設定 */
for(j = 1; j <= N; j++)
{
x = (j-0.5)*h;
u[j] = 2*x*(1 - x);
}
u[0] = -u[1];
u[N+1] = -u[N];
/* 時間方向へのループ(アニメーション)*/
for(k = 0; k <= M; k++)
{
t = k*tau;
/* INTV 間隔でグラフを表示 */
if( k%INTV == 0 )
{
/* 黒縁,白の長方形を描く(一つ前の時間のグラフを消す) */
g_line_color(G_BLACK);
g_line_width(2.0);
g_area_color(G_WHITE);
g_box(0.0, L, 0.0, 1.0, G_YES, G_YES);
/* 配列 u をグラフとして描く */
g_line_color(G_RED);
g_line_width(1.0);
g_area_color(G_WHITE);
g_data_plot(0.0, L, u, N+1);
if( k == 0 )
{
/* 初期値を良くみたいので */
/* 初期値の場合は表示しクリックを待つ */
g_sleep(G_STOP);
}
/* 初期値以外の場合は 0.01 秒間止る */
/* これによりアニメーションのちらつきをある程度おさえる */
else
{
g_sleep(0.01);
}
}
/* 空間方向へのループ */
/* 時間を1ステップ進める */
/* アルゴリズム1の赤字の部分 */
/* ヒント:2つの for 文 */
u[0] = -u[1];
u[N+1] = -u[N];
}
/* 計算終了後マウスがクリックされるまで停止 */
g_sleep(G_STOP);
g_term();
}
上のプログラムの抜けている部分をうめてプログラムを完成させよ.
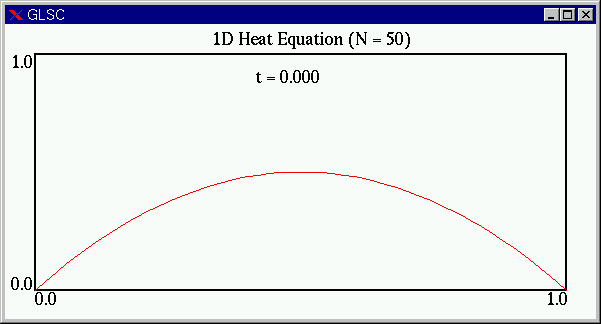
実際の計算部分を正しくプログラムにすることができれば,次のようなアニメーションを見ることができます.両端から熱が奪われ,全体の温度が下がることがわかります.
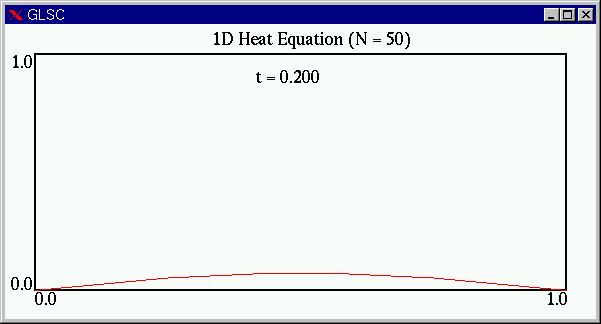
次の問題を考えます.先の問題0.1.1と少し違いますので注意してください(初期値と x の範囲が異なる).
問題 0.2
課題2
問題0.2の解を数値的に求めるプログラムを作成してください.πは3.1415926等と近似値を与えてください.
先に出てきた,
を繰り返し計算し,近似解を求める方法を陽解法と呼びます.(前の時刻 tn での値から次の時刻 tn+1 の値を直ちに計算できる形の差分方程式を陽公式(explicit scheme)と呼びます.陽公式を使った解法なので陽解法と呼びます.)
天下り的になりますが,拡散方程式の数値解法として陽公式を用いる場合, τと h と D は次の関係を満たす必要があります(安定性条件).
α = Dτ/h2 < 1/2 (S)
ここでは,この安定性条件を破った場合に計算がどのようになるかを見ます.
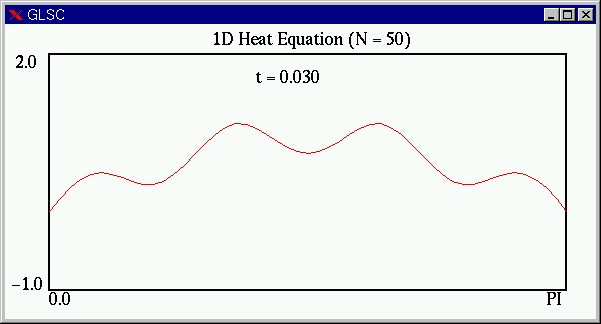
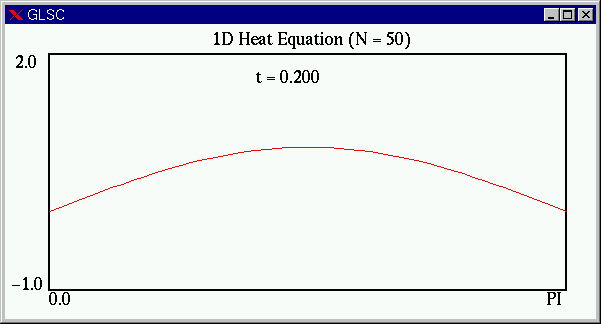
課題2計算結果から熱方程式の解の性質についてわかることをまとめよ.講義で習った解析解(微分解)からわかる性質を再現しているか?(例えば,波数の多いものほど早く減衰するなど.近似解であって欲しいので,当然再現していてもらわないと困る.)
課題1,課題2にて作成したプログラムが上記安定性条件(S)を満たしていることを確かめよ.
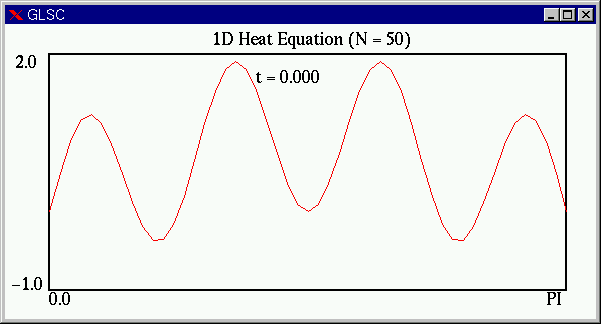
課題5に従い,安定性条件(S)をわずかに破った場合,次のような結果が得られます.(S)の左辺の値が 0.5066 と,1/2 をわずかに越えているにすぎませんが,最終的には真の解からはほど遠いギザギザの状態になってしまいます.1/2 を大きく越えると,計算がおかしくなるのも早まります.(ここでは n および M をα>1/2 となるように調整した.)
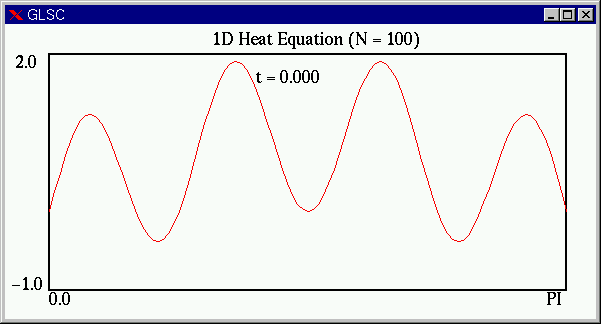
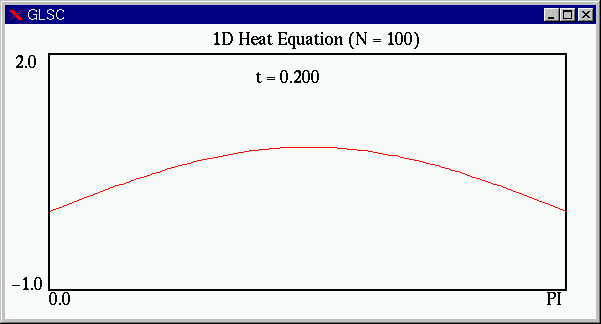
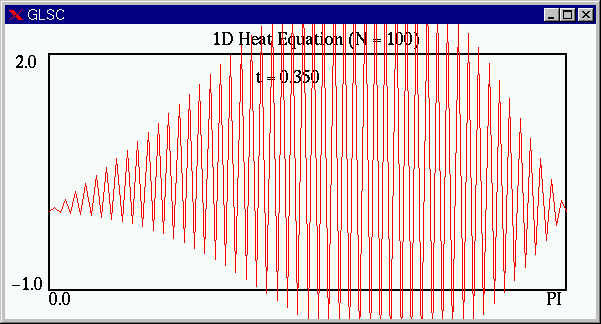
上の,ギザギザの解は,直感的に考えても熱方程式の解としてはおかしいことがわかると思います.(スプーンの熱分布がこの様になるとは思えません.)陽解法においては安定性条件を満たさないパラメータで計算すると,計算が不安定となり,上記のような現象が見られます.(ただし,これは,差分方程式の解としては正しいものです.しかし,近似したい熱方程式の近似解とはなっていところが問題なのです.)
注意: 上の計算結果では対称製の崩れ(初期値は π/2 で対称)がみられます.これは,πを近似値として与えたためであると思われます.
この様に,陽解法においては,計算が安定に進むためには時間刻み幅および空間刻み幅が安定性条件(S)を満たさねばなりません.ところが,この条件は計算量の点で問題があります.例えば,時刻0から1まで計算を行うとします.時間方向の格子点の総数は 1/τとなります.計算の手間(計算時間)を減らす為には τ をなるべく大きく取りたい(τ が大きければ少ない繰り返し計算で目的の時刻まで計算できるので).そこで,安定性条件(S)より,
τ ≒ h2/(2D)
とすれば良いでしょう((S)を余裕をもって満たす τ を用いる).一方,D は一定とした場合,精度の良い計算をするために空間に関する分解能を高めたいとします.そこで h を 1/10 倍にしたとします.すると,τ は上の関係から 1/100 倍せざるを得ません.ということは,時間方向の格子点数が 100倍 に増えることになります.これでは, h を小さくしていったときに,あまりに格子点数が多くなりすぎて計算の効率が悪くなります.例えば今の例では,h を 1/10 倍したため,計算量は 10 倍となり(これは仕方が無い),更に安定性条件(S)を満たすために τ を 1/100 倍したので計算量は更に100倍となりました.つまり,もとの計算量に比べて 1000倍の計算量が必要(1000倍時間がかかる!)となります.
つまり,陽解法では,空間解像度を細かくしたい場合に,時間刻み幅もそれにあわせて変更する必要があります.できることならそういう事を気にせずに(全く気にしなくても良いわけではありませんが・・)自由に空間解像度を上げ下げしたいものです.その要求を満たす解法として陰解法と呼ばれる方法があり,陰解法は無条件安定であることがわかっています(安定な計算に対するαに関する条件が無い).(演習では時間の関係から陰解法についてはできませんが,各人陰解法のプログラムの作成をしてみることをおすすめします.陰解法では連立一次方程式を解く必要がありますが,それらのプログラムは良いプログラミングの練習にもなります.)
次の問題を考えます.
問題 0.3
u(x,t) = sin(3πx)exp(-(3π)2t) (5)
が,問題0.3の解であることを確かめよ.
問題 0.3を数値計算で解いた差分解と微分解(5)を比べることで,差分法による計算が,どの程度解析的に求まった解(5)と近いのかを調べる.直感的には h や τ を小さくすると,近似の程度はよくなると思われるが,実際どの程度よくなるかを確かめる.
問題0.3を数値計算で解いた解を u kj とし,解(5)の格子点状での値を,u(xj, tk) と書くとき,それらの相対誤差を次のように定義します.
(6)
もしも,数値計算で求まった解と,解析的に求まった解が完全に一致していれば err(N) は 0 となりますが,実際にはなりません.N (空間刻み数)を変化させて,相対誤差がどのように変化するかを見ましょう.
err(N) は k (時刻)を止めるごとに求まりますが,ここでは k=M とすることにします.ただし M とは T を時間の上限とした場合の M=T/τ.
N を色々かえてみて err(N) を求めればよいのですが,上で紹介した安定性条件(S)があるために,N を独立に自由に動かすことはできません.
α = Dτ/h2 < 1/2 (S)
h は N と L (N:空間分割数 ,L:領域長)から決まりますが,いま L=1 としますから,h は N からのみ決まることになります.(S)を満たしていなければならないので,ひとまず,
α=1/3
としましょう(ここに 1/3 は 1/2 より小さければ何でも良い訳で特別意味は無い).すると,
τ=h2/3
となります.t の上限である T を与えれば次の式で時間刻み数 M を得ることができます.
M=T/τ
先に示したプログラムでは,N, M, T から τ, αが決まっていましたが,今回は α, n, T からM, τが決まります.
解を求める時刻の上限を T ,空間刻み数を N とし,αは1/3とすることにすると,アルゴリズムは次のようになります.前回のプログラムを変更すればよいのですが(変更にはプログラムの理解が必要),新たに double U[IMAX+2] という配列が必要になります(微分解の値をいれる配列.差分解と比較するために必要).
(1)初期パラメータ設定
N, T, α を設定する
α:=1/3, h := 1/N, τ:=αh2, M:=T/τ
(2) 初期値設定
j := 1,....,N の順に
uj := sin(3πxj)
Uj := sin(3πxj)を繰り返す
u0 := -u1, uN+1 = -uN (境界条件)
(3)
k := 1,.....,M-1 の順に
tk := kτ
j := 1,2,....,N の順に
new_uj := αuj-1 + (1 - 2α)uj + αuj-1
を繰り返す
j := 1,2,....,N の順に
uj := new_uj
を繰り返す
u0 := -u1, uN+1 = -uN (境界条件)
j := 1,2,....,N の順に
xj := (j - 0.5)*h
を繰り返す
一定間隔ごとに u1〜uN, U1〜UN を画面に表示
を繰り返す
(4)
をもとめ, h と err を画面に表示する
途中 max なるものがあるが,これは最大値を求める事と同じ事なので,これまで通り for 文と if 文の組み合わせで求めることができる. max なる標準関数は無いので注意すること.
上記アルゴリズムにそったC言語のプログラムを作成せよ.GLSCでグラフを描いてもらうが,uj を赤色の線,Uj を青色の線で描け(uj, Uj)はそれぞれアルゴリズム2中の表記による).(L = 1.0 としたが,さらに T = 0.05 とすることにする.L は領域の大きさであり,T は時間の上限)
N = 50, 100, 200, 400 についてそれぞれ err(N) を求め,h と err(N) の間にどのような関係があるか調べて見よ.
課題8の結果を err.data として保存せよ(方法は色々あるが,最も安易な方法は,表示されたデータをテキストエディタで打ち込む事である).ただし,ファイルの内容は,全部で4行のテキストファイルで,各行にはそれぞれ,h と対応する err(N) の値をスペース一文字となるようにすること.例えば,次のようになる.(以下の出力は %e にて浮動小数点形式で表示したもの.)
2.000000e-02 2.474867e-02
1.000000e-02 6.233837e-03
5.000000e-03 1.567177e-03
2.500000e-03 3.813807e-04
課題9で作成した err.data を gnuplot でグラフ化する.ターミナル上で gnuplot と打ち込み,gnuplot を起動した後,gnuplot> というプロンプトが表示されるので,そこで,
plot 'err.data' with linespoints
とすれば,グラフが表示される.gnuplot は gnuplot> のプロンプトに対して, quit と打ち込むことで終了することができる.
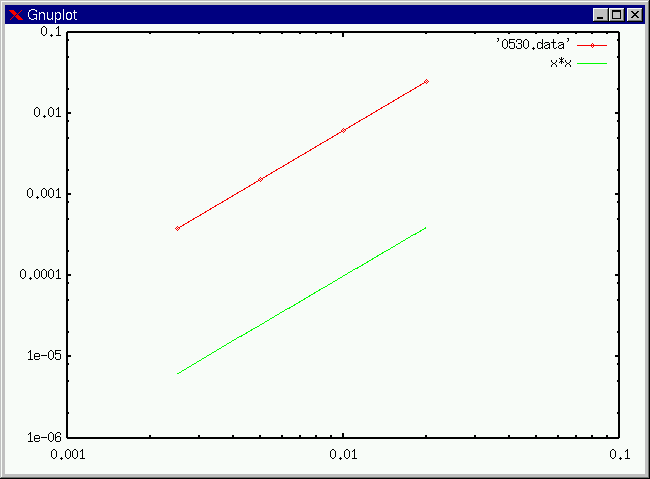
グラフから,h を 1/2 にすると err(N) は 1/4 となることを確かめたい(つまり,err(N) が h*h に比例しているという事実).その為に,グラフを両対数グラフとし,あわせて y = x*x のグラフを重ねることで視覚的に確かめる.gnuplot を起動し次のコマンドにて両対数グラフを表示することができる.
set logscale
plot 'err.data' with linespoints, x*x
結果は例えば次のようになる.離散化の過程で見たように,真の解との誤差は h*h に比例すると考えられたが,実際そのようになっていることを確かめることができる.もしも,x*x の直線と違う傾きの直線なり曲線になった場合は,プログラムのミスである可能性が高い.この様に,プログラムのミスを発見する一つの有用な手段になりうる.
問題0.3の初期値が
の場合(これを問題0.3.1としよう),
が問題0.3.1の解であることを示せ.
課題12の初期値を採用し,その中の K や N を色々かえると(ただし,この N は sin 関数内の N であって,空間刻み数では無い),err はどのようにかわるか調べよ.