前回に引き続き,GLSCグラフィックライブラリの使い方について説明します。今回扱う「仮想座標系」はつまずきやすいポイントです.よく理解してください.できるだけわかりやすいように口頭で例を交えながら説明するつもりです.ホームページ内容を良く読んでも意味がわからない人は口頭説明をよく聞いてください.
GLSCでは、前回でてきた標準座標系の他に仮想座標系を定義し利用することができます。しかも、仮想座標系はいくつでも(もちろん限界はありますが)定義することができます。仮想座標系を定義するには g_def_scale という関数を使います。
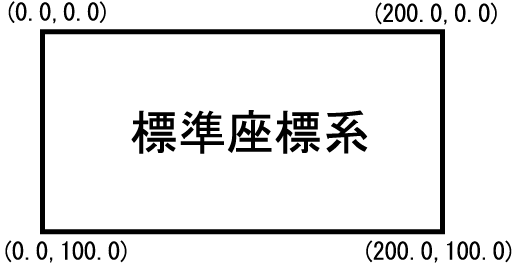
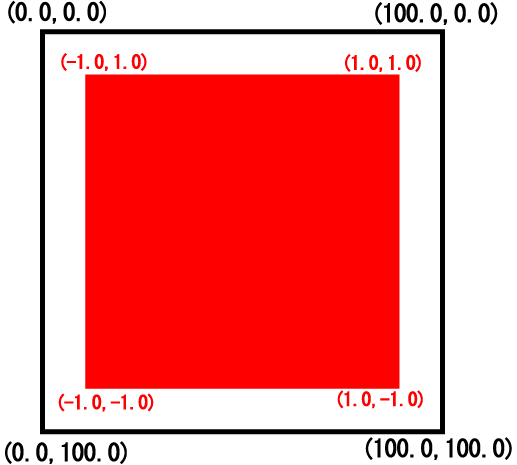
前回あつかった標準座標系は、例えば g_init("GRAPH", 200.0, 100.0) と初期化されたウィンドウでは次の図のようになりました。

つまり、左上が座標 (0.0, 0.0) であり、右下が (200.0, 100.0) となるような座標系です。例えば、 y = sin(x) のグラフを 0 < x < 4 の範囲で描きたい場合、標準座標系にそのようなグラフを描くには、座標変換の手続きが必要となります。それでは、いちいち紛らわしいので、この場合次のような座標系となっていれば便利です。(GLSCが自動的に座標変換を行ってくれるということです.)
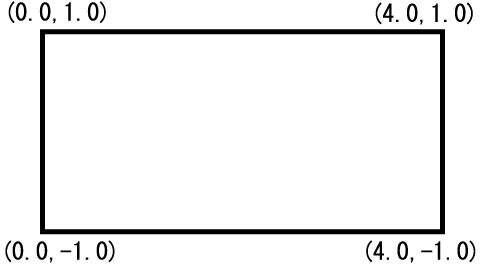
座標系がこのようになっていれば、y = sin(x) のグラフを描くのが簡単です。実は、GLSCでは、このような座標系を、先の GLSC ウィンドウ内にいくつでも作ることができます。そして、実際に GLSC で絵を描く場合、この座標系(仮想座標系と呼びます)を用います。先の標準座標系は、文字列の描画時と仮想座標系の定義時にのみ使います。(仮想座標系を GLSC ウィンドウ内に定義する場合には何らかの座標系が必要です。標準座標系はその為にあるものだと考えてください。)
例えば、先の標準座標系の中に、1つの仮想座標系を定義した場合のイメージを次に示します。
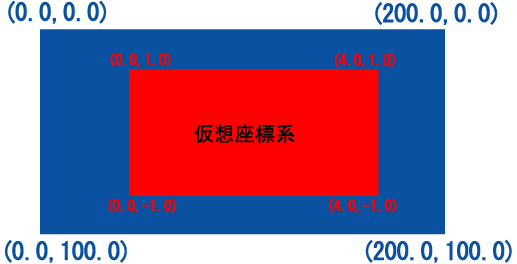
青色が、GLSCウィンドウ全体をあらわしています。その中に赤色の仮想座標系が定義されている様子を示しています。このような仮想座標系は次の g_def_scale 関数を用いて定義することができます。
GLSC ウィンドウ内に長方形領域を定義して、その長方形内の座標系を定義する関数が g_def_scale 関数です。GLSC ウィンドウ内に長方形を定義するには長方形の位置、大きさを指定する必要があります。また、新たに作成する仮想座標系の左端、右端、下端、上端の値を指定する必要があります。つまり、長方形の位置と大きさを指定するために4つの値が必要であり、新座標系を指定するために4つの値が必要(計8つ!)となるということを理解すれば、g_def_scale 関数に多くの引数の意味がおのずとわかります。また、仮想座標系はいくつでも定義できるので、どの仮想座標系の定義であるかを示す通し番号も必要となります。つまり、g_def_scale 関数には、全部で9つの引数があります。
GLSCマニュアルの g_def_scale 関数の説明部分は次のように記載されています。このように、GLSC の関数は引数が多いので、関数利用の際には各人マニュアルを参照してください。
g_def_scale
はじめの引数は、これから定義する仮想座標系につける通し番号です。2,3,4,5番目の引数は、仮想座標系の左端、右端、下端、上端の値であり、6,7,8,9番目の引数は、仮想座標系の位置と大きさを標準座標系で与えます。長方形の位置と大きさは、4頂点の座標を与えるのではなく、長方形の左上の標準座標系での座標と、長方形の幅と高さを与えるというところに注意してください。 では、実際に g_def_scale
関数をつかったサンプルプログラムを見てみましょう。 #include <glsc.h> このプログラムでは、次のような仮想座標系を定義しています。 GLSC では g_circle 関数で円を描画することができます。g_circle
には5つの引数があり、はじめの2つで、円の中心位置を仮想座標系にて指定します。3つめの引数は、描く円の半径。4つめの引数は円のふちを描くかどうかの指定(G_YES
または G_NO)で、5つめの引数は、円の内部を塗りつぶすかどうかの指定(G_YES
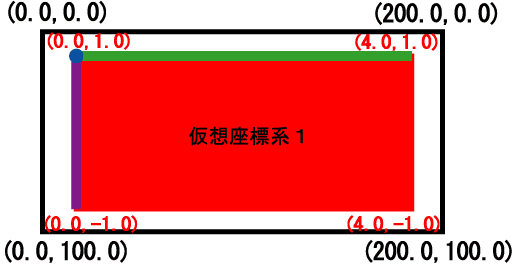
または G_NO)を行います。 #include <glsc.h> 上のプログラムでは、次のような仮想座標系(赤色で示した)を1番(g_def_scale
の第一引数)として定義しています。その仮想座標系に絵を描きたいので、それを選ぶために
g_sel_scale 関数で1番の仮想座標系を選びます。その後、g_circle
関数で円を描きます。このように、仮想座標系がたった一つであっても、g_sel_scale
で一度選ぶ必要があります。g_def_scale
関数と g_sel_scale 関数は GLSC
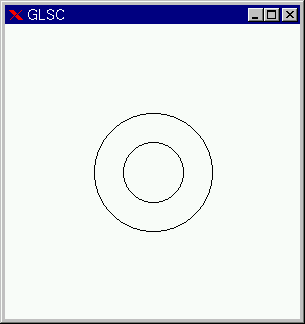
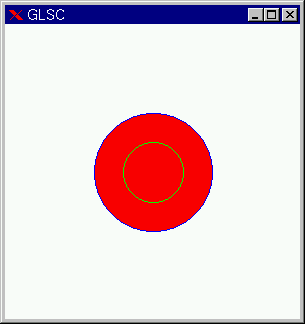
プログラムには必ず出てくると思ってください。 プログラムの実行結果は次のようになります。 2つの仮想座標系を定義して、使ってみましょう。次の例では、標準座標系上の全く同じ位置に同じ大きさの仮想座標系を作っています。ただし、座標のスケールが異なります。 #include <glsc.h> 実行結果は次のようになります。2つの g_circle は全く同じなのに(位置、半径が同じ)、2つの見た目違う半径の円が描かれました。異なる仮想座標系を用いて描いているからですが、その意味をよく理解してください。 (仮想座標系をうまくとれば,楕円が描けそうな気がしますが,残念ながら描けません.) 円に色をつけることもできます。g_area_color
関数で、円内部の塗りつぶし色を指定し、g_line_color
関数でふちの線色を指定します。2つめの g_circle
では、内部塗りつぶしをしない(5つめの引数が G_NO
である)ので先に描かれた赤色が残っています(5つめの引数を
G_YES に変更してみよ)。 #include <glsc.h> g_box 関数により、四角形を描くことができます。g_box 関数の使い方はGLSCマニュアルを参考にしてください。 ちょっとしたテクニック:前回でてきた,g_cls() 関数は,画面全体を覆うような白い四角形を描くことと同等です.つまり,絵柄を部分的に消去したい場合には,背景色と同じ色で塗りつぶされた四角形や円を描けば良いでしょう.全体を消すよりも,消したい部分だけを消す方が高速であるから,ちらつき防止となり,結果としてなめらかなアニメーションとなります. 練習問題:赤く塗りつぶされた1つの小さな四角形が画面上を移動するアニメーションを,g_cls()関数を使わずに作ってみよ. g_move 関数と g_plot
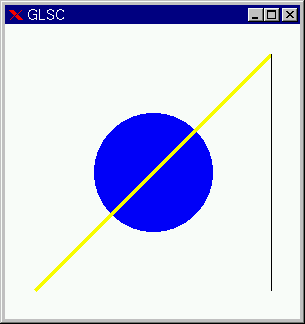
関数を用いると直線を描くことができます。g_move
関数で直線の始点を指定し、g_plot
関数で直線の終点を指定します。また、g_line_color
関数で、直線の色を指定でき、g_line_width
関数で直線の幅を指定できます(それぞれマニュアル参照)。 #include <glsc.h> g_plot
を連続してプログラム中に書くと、連続した直線を描く事ができます。直前のプログラムの2つめの
g_move
を消去した次のプログラムでは、次のような結果となります(実際に2つめの
g_move 関数を消去して試してみよ)。 つまり、直前の g_plot
関数で指定された座標を始点とする直線が引かれます。 課題1 複数の仮想座標を定義し、それぞれに対し円や長方形を描画せよ。 課題2 円や長方形を組み合わせて、なにか面白い絵を描け。 課題3 円が時間と共に移動するアニメーションプログラムを作成せよ。 これから、GLSCを使って y = sin(x) のグラフを描きます。実際には y =
sin(x) のグラフは滑らかな曲線ですが、コンピュータではそのような滑らかな曲線を直接は扱えませんので折れ線で近似します。つまり、変数
x は、実際には連続的に変化するものですが、とびとびの値を使います。後の例で見るように、とびとびとはいえ、十分に細かく取れば、折れ線で曲線をうまく近似することができます。 図のように [0, L] 区間を N-1 等分して、その等分した小区間の幅を
dx とします。N-1 等分すると図のように N
個の区切りが現れますが、それらに 0,1, ...., i, ...., N-1
と番号をつけることにします。また、 N を分割数、 dx
を分割幅と呼びます。このとき、 Xi = i*dx の部分についてそれぞれ y = sin(Xi)
を計算し、それらを折れ線で結ぶことを考えます。C言語風に書けば X[i] = dx*i; をそれぞれ求め、(X[0], Y[0]), (X[1],Y[1]), ...., (X[N-1], Y[N-1]) を結ぶ折れ線を描くことになります。これをプログラムにすると次のようになります。(上記の説明にあわせるためにかなり無駄なことをしています。)ファイル名を 0426-1.c として打ち込み、実行してみてください。 注意: 数学関数(sin, cos, tan 等)を使う場合には #include <math.h>
が必要となります。 #include <glsc.h> 上記プログラムに、グラフの左端右端等の情報を書き入れたプログラムの出力を使って、N
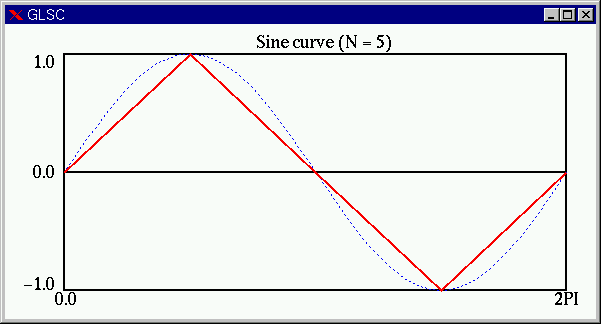
とグラフの関係を見てみましょう。青色の破線で書かれたグラフが描きたいグラフ
(y = sin(x) )です(とはいっても、もちろんこれも N=100
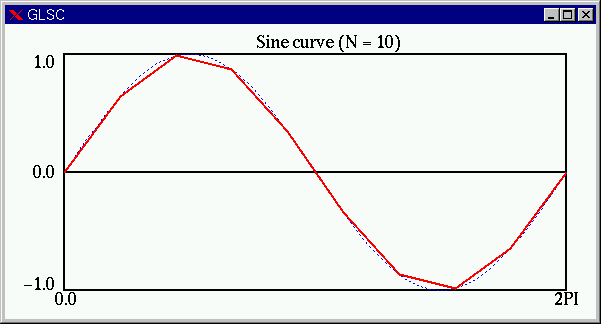
の折れ線です)。赤色の実線が描こうとしている折れ線です。 N=5 の場合は次のようになります(赤線)。これでは、まったく
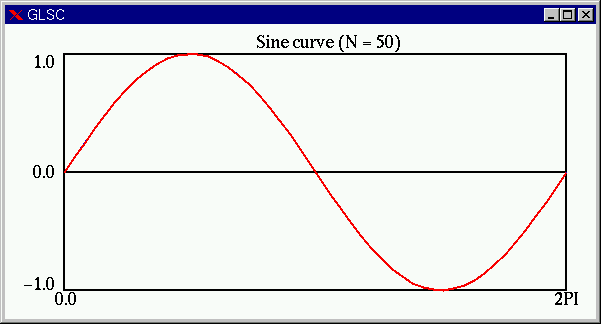
y = sin(x) のグラフには見えません。 つづいて、N=10 の場合(赤線)。曲線っぽくみえてきました。 N=50 の場合(赤線)。見た目はほぼ
y=sin(x)
のグラフに見えます。 先のプログラム例では、 g_move および g_plot
関数を用いてグラフを描いていましたが、GLSCにはグラフを描く為のg_data_plot
関数が用意されているので通常それを用います。g_data_plot 関数を用いた同様のプログラムを次に示します。先のプログラムにはあった X[N] の配列は不要なのでなくしました(先のプログラムでも実際には X[N] の配列は不要でした)。ファイル名を 0426-2.c として打ち込み、実行してみてください。 #include <glsc.h> g_data_plot
関数には4つの引数があります。1番目、2番目の引数は仮想座標系における左端および右端の値、3つめはこれから描くグラフの
y 座標が格納されている配列名(今の場合、配列を Y[N]
で定義しているので、 Y
が配列名となる)。4つめは配列のサイズ(整数)となります。詳しくはマニュアルを参照してください。 課題4 上のサンプルプログラム(0426-2.c)を表示例のように表示するプログラムに変更せよ。(グラフの左端等の表示とN=100のグラフを重ねて表示するように変更) ヒント: Y[N] とは別に Y0[100]
という配列を作って、それぞれを異なる線種で g_data_plot
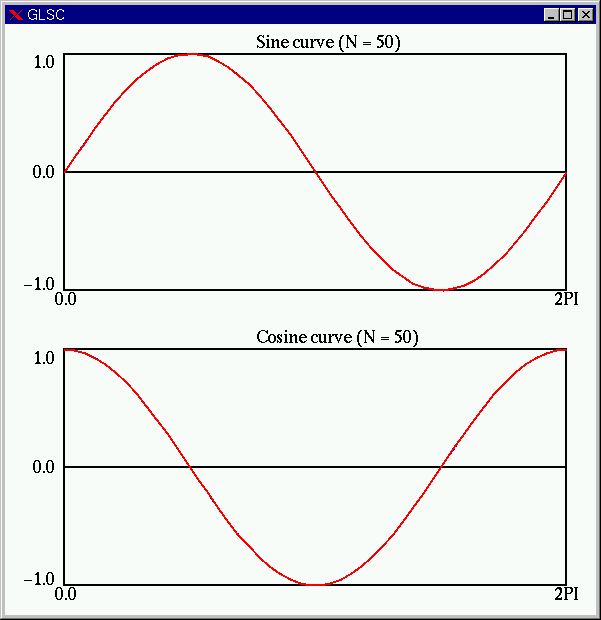
を用いて描く。また、文字列の描画(その2)で説明した手法を用いてタイトル部分を書くと良い。 課題5 仮想座標系を2つ用意し、下の図のように、y = sin(x) のグラフと y =
cos(x)
のグラフをそれぞれの仮想座標系に対して描け。(必ず仮想座標系を2つ用意すること。) すでに、アニメーションの作り方を知っているので簡単です。ただし、いま
t
は時間として扱いますが、当然連続量として扱うことができないので、x
同様とびとびの値として扱います。先ほどの x
と同様に考え、t の範囲を [0, T] として、それを K-1
等分します。その小区間の幅を dt として(つまり、 dt =
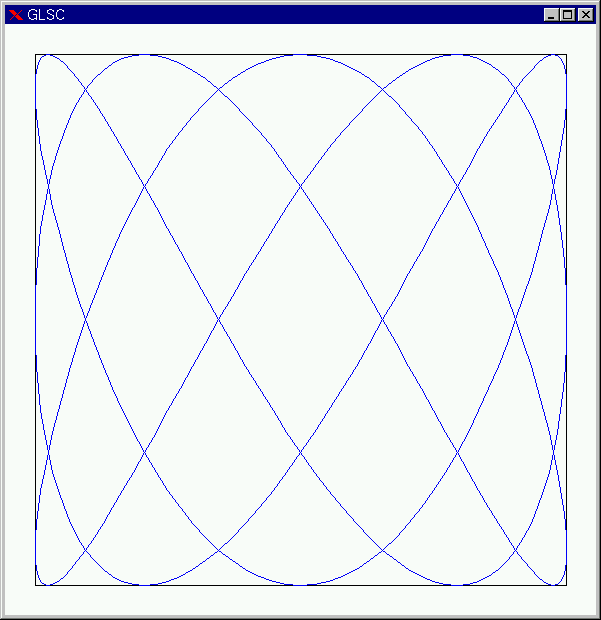
T/(K-1))、 Tk = dt*k とすることにより、 Tk を止めるごとに Y[i] = sin(Xi + Tk) のグラフを描くことを繰り返せば、アニメーションとなります。次のサンプルプログラムを 0426-3.c として打ち込み実行してみてください。これまでのアニメーションプログラムと仕組みが同じであることに気づくことが重要です。 #include <glsc.h> 課題6 上のサンプルプログラム(0426-3.c)で N を 5 にするとどうなるか?やってみよ。 課題7 上のサンプルプログラム(0426-3.c)にグラフの左端等の情報を表示する部分を追加せよ。 課題8 次の図を描くプログラムを作成せよ。 課題9 ~daishin/sample/liss ~daishin/sample/liss2 をそれぞれ実行し、それらと同じ動きをするプログラムを作成せよ。 liss2 は liss を少し変更したもの. 以下に、C言語の復習用にいくつか課題を載せておきます。 課題1 以下のプログラムはどのように動作するかまえもって予想し、実際に実行してみよ。 1: #include <stdio.h> 課題2 円の半径を入力すると、円の面積および円の円周を計算して両方を画面に表示するプログラムを作成せよ。 課題3 以下のプログラムは、入力された西暦年が閏年かどうかを判定するプログラムである。以下のプログラムが正しいとして、閏年であるかどうかは、どのような計算により判定できるか答えよ。また、以下のプログラムでは、if
文を二度用いているが、一つの if 文にまとめよ。 #include <stdio.h> main() 課題4 以下のプログラムはどのように動作するかまえもって予想し、実際に実行してみよ。wa
= 0; seki = 1; としてあるのは何故か? #include <stdio.h> main() 課題5 整数 n を入力すると 1〜n
までの積(階乗)を計算し表示するプログラムを作成せよ。 課題6 正の整数を1つ入力すると、その数が素数かどうかを判定して表示するプログラムを作成せよ。 課題7 正の整数 n を入力すると n
以下の素数を全て表示するプログラムを作成せよ。 課題8 次の仕様を満たす関数を作成し、それを使うプログラムを作成せよ。 関数名: int sosu(int n) 仕様: 引数として整数 n
を受け取り、それが素数であれば戻り値として 1 を返し、n
が素数ではないまたは負である場合には -1 を返す 課題9 課題6,7のプログラム(素数判定プログラム)を課題8で作った関数を使うものに変更せよ。 課題10 フィボナッチ数列は
からはじめて、漸化式
で作られる数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, .... のことである。整数 m
を入力すると F m+2
までのフィボナッチ数列を表示するプログラムを作成せよ。ただし、配列は使わないこと。あまり大きな
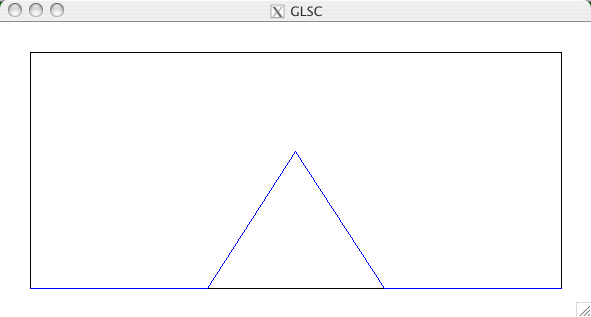
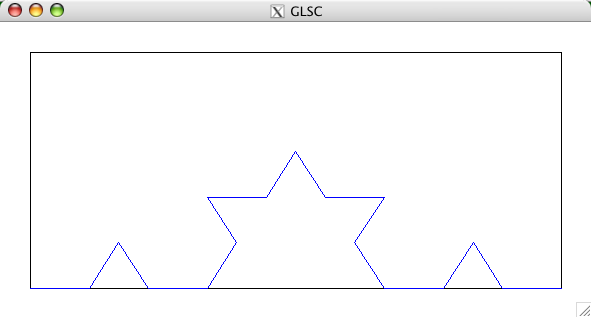
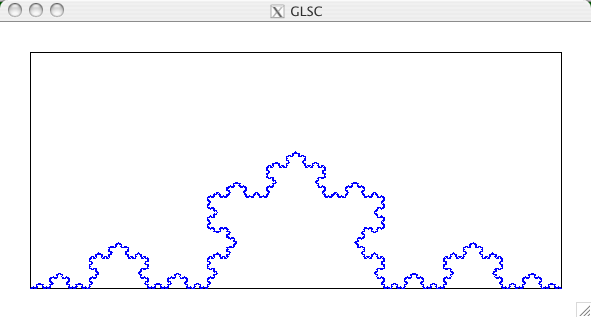
m については、正しい数値が得られないことを確認せよ。 グラフィックスを用いる練習課題 コッホ曲線とは、 1.直線を引く 2.直線を3等分する 3.その分割した2点で正三角形をつくる 4.出来上がった各小区分について2,3を繰り返す により得られる図形です。上記手続きを適当な回数繰り返して得られる図形を描くGLSCのプログラムを作成してください。以下にそのようなプログラムの実行例をあげます。 青い直線を3等分し、分割した2点で正三角形を作ったところ。4つの小区分にわかれた。 上でえられた4つの小区分にたいして、同様の手続き(それぞれの小直線を3等分し、分割した2点で正三角形を作る)を経て得られた図形。16小区分により構成される図形となる。次は同様に、その16区分全てについて同様の手続きを行う。これを繰り返す。 上記手続きを数十回繰り返した後得られた図形。
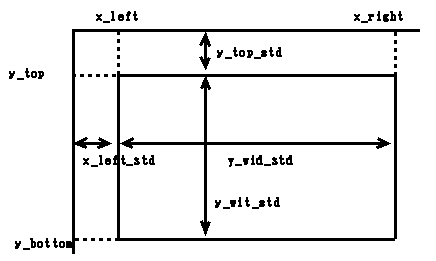
scale
整数
スケール番号。50個まで仮想座標系を
導入することができる。( 0 ≦ scale ≦ 49 )
x_left
実数
長方形の左辺の仮想座標系におけるx座標
x_right
実数
長方形の右辺の仮想座標系におけるx座標
y_bottom
実数
長方形の下辺の仮想座標系におけるy座標
y_top
実数
長方形の上辺の仮想座標系におけるy座標
x_left_std
実数
長方形の左辺の標準x座標
y_top_std
実数
長方形の上辺の標準y座標
x_wid_std
実数
長方形の標準面上でのx軸方向の幅
y_wid_std
実数
長方形の左辺の標準y軸方向の幅
下図のように適当な長方形を考えて,上記描くパラメータを定めることにより仮想座標系を決める。
#include <stdio.h>
main()
{
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
g_def_scale(1, 0.0, 4.0, -1.0, 1.0, 10.0,
10.0, 180.0, 80.0);
g_sleep(G_STOP);
g_term();
}
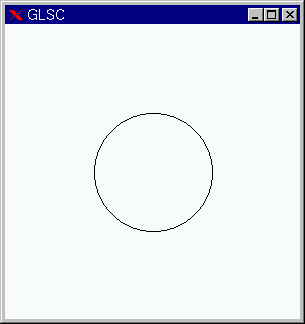
円の描画
#include <stdio.h>
main()
{
g_init("GRAPH", 100.0, 100.0);
g_device(G_DISP);
g_def_scale(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 80.0, 80.0);
g_sel_scale(1);
g_circle(0.0, 0.0, 0.5, G_YES, G_NO);
g_sleep(G_STOP);
g_term();
}
#include <stdio.h>
main()
{
g_init("GRAPH", 100.0, 100.0);
g_device(G_DISP);
g_def_scale(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 80.0, 80.0);
g_def_scale(2, -2.0, 2.0, -2.0, 2.0, 10.0, 10.0, 80.0, 80.0);
g_sel_scale(1);
g_circle(0.0, 0.0, 0.5, G_YES, G_NO);
g_sel_scale(2);
g_circle(0.0, 0.0, 0.5, G_YES, G_NO);
g_sleep(G_STOP);
g_term();
}
#include <stdio.h>
main()
{
g_init("GRAPH", 100.0, 100.0);
g_device(G_DISP);
g_def_scale(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 80.0, 80.0);
g_def_scale(2, -2.0, 2.0, -2.0, 2.0, 10.0, 10.0, 80.0, 80.0);
g_sel_scale(1);
g_area_color(G_RED);
g_line_color(G_BLUE);
g_circle(0.0, 0.0, 0.5, G_YES, G_YES);
g_sel_scale(2);
g_area_color(G_GREEN);
g_line_color(G_GREEN);
g_circle(0.0, 0.0, 0.5, G_YES, G_NO);
g_sleep(G_STOP);
g_term();
}
四角形の描画
直線の描画
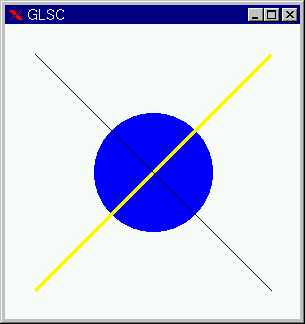
#include <stdio.h>
main()
{
g_init("GRAPH", 100.0, 100.0);
g_device(G_DISP);
g_def_scale(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 80.0, 80.0);
g_sel_scale(1);
g_area_color(G_BLUE);
g_line_color(G_BLUE);
g_circle(0.0, 0.0, 0.5, G_YES, G_YES);
g_line_color(G_YELLOW);
g_line_width(3);
g_move(-1.0, -1.0);
g_plot(1.0, 1.0);
g_line_color(G_BLACK);
g_line_width(1);
g_move(-1.0, 1.0);
g_plot(1.0, -1.0);
g_sleep(G_STOP);
g_term();
}
y = sin(x) のグラフの描画
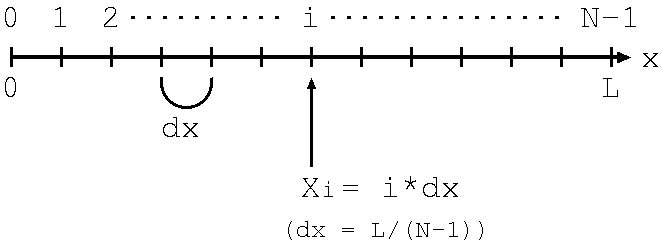
Y[i] = sin(X[i]);
#include <stdio.h>
/* 次の文は数学関数を使う場合に必要 */
#include <math.h>
/* 定数の定義 */
#define N (5)
#define PI (3.1415926)
#define L (2*PI)
main()
{
int i;
float X[N], Y[N], dx;
/* dx を求める */
dx = L/(N - 1);
/* GLSCの初期化および仮想座標系の定義 */
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
/* 外枠の描画 */
g_sel_scale(1);
g_area_color(G_WHITE);
g_line_color(G_BLACK);
g_line_width(2);
g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
g_move(0.0, 0.0);
g_plot(L, 0.0);
/* X[i] を求める */
for(i = 0; i < N; i++)
{
X[i] = i*dx;
}
/* Y[i] を求める */
for(i = 0; i < N; i++)
{
Y[i] = sin(X[i]);
}
/* 折れ線を描く */
g_line_color(G_RED);
g_line_type(G_LINE_SOLID);
g_line_width(2);
g_move(X[0], Y[0]);
for(i = 1; i < N; i++)
{
g_plot(X[i], Y[i]);
}
g_sleep(G_STOP);
g_term();
}
#include <stdio.h>
#include <math.h>
/* 定数の定義 */
#define N (5)
#define PI (3.1415926)
#define L (2*PI)
main()
{
int i;
float Y[N], dx;
/* dx を求める */
dx = L/(N - 1);
/* GLSCの初期化および仮想座標系の定義 */
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
/* 外枠の描画 */
g_sel_scale(1);
g_area_color(G_WHITE);
g_line_color(G_BLACK);
g_line_width(2);
g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
g_move(0.0, 0.0);
g_plot(L, 0.0);
/* Y[i] を求める */
for(i = 0; i < N; i++)
{
Y[i] = sin(i*dx);
}
/* 折れ線を描く (g_data_plot)*/
g_line_color(G_RED);
g_line_type(G_LINE_SOLID);
g_line_width(2);
g_data_plot(0.0, L, Y, N);
g_sleep(G_STOP);
g_term();
}
y = sin(x + t) のグラフのアニメーション
#include <stdio.h>
#include <math.h>
/* 定数の定義 */
#define N (50)
#define K (100)
#define PI (3.1415926)
#define L (2*PI)
#define T (10.0)
main()
{
int i, k;
float Y[N], dx;
float dt;
/* dx, dt を求める */
dx = L/(N - 1);
dt = T/(K - 1);
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
/* 仮想座標系の定義 */
g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
g_sel_scale(1);
for(k = 0; k < K; k++)
{
/* 外枠の描画 (グラフの消去) */
g_area_color(G_WHITE);
g_line_color(G_BLACK);
g_line_width(2);
g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
g_move(0.0, 0.0);
g_plot(L, 0.0);
/* Y[i] を求める */
for(i = 0; i < N; i++)
{
Y[i] = sin(i*dx + k*dt);
}
/* 折れ線を描く (g_data_plot)*/
g_line_color(G_RED);
g_line_type(G_LINE_SOLID);
g_line_width(1);
g_data_plot(0.0, L, Y, N);
g_sleep(0.05);
}
g_sleep(G_STOP);
g_term();
}
C言語復習用課題
2:
3: main()
4: {
5: float pi, r, s;
6:
7: pi = 3.14159;
8:
9: printf("円の半径を入力してください:");
10: scanf("%f",
&r);
11:
12: s = pi*r*r;
13:
14: printf("円の面積は
%f です。\n", s);
15: }
{
int n;
printf("年=");
scanf("%d", &n);
if ((n%4 == 0) && (n%100 != 0))
{
printf("うるう年です\n");
}
if (n%400 == 0)
{
printf("うるう年です\n");
}
}
{
int i, wa, seki;
wa = 0;
seki = 1;
for (i = 1; i <= 5; i++)
{
wa = wa + i;
seki = seki*i;
}
printf("和=%d\n", wa);
printf("積=%d\n", seki);
}
![]()
![]()