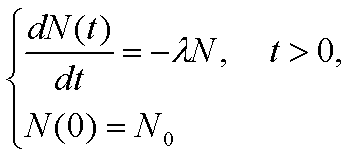 (P)
(P)前回,口頭にて指示しましたが,前回作業しなかった人は以下の内容に従って,レポート提出の準備を行ってください.
計算数学演習を受講しなかった人は、ファイルマネージャーを用いて、 report および work という名前のフォルダをホームディレクトリ(ホームフォルダー)に作成してください。
以前、計算数学演習を受けていた人は、既に work および report フォルダがあると思います。それらをそれぞれ、work_old および report_old と名前を変えてください。その後、新規に report および work フォルダを作成してください。
以下、より丁寧な説明を書いておきます。よくわからない人は、我々に質問してください。
端末室のパソコンにログインした直後には、ファイルマネージャーが起動しているはずです。これを用いて、フォルダーをつくり、これまで作ってきたファイルをフォルダー内にまとめましょう。ファイルマネージャーの使い方の詳細は備え付けのマニュアルにまかせます。work というフォルダーを作成し、先々週作成したファイルを移動してください。また、自動回収によるレポート提出の為のフォルダー(reportという名前のフォルダー)を作成してください。
以前、計算数学演習を受けていた人は、既に work および report フォルダがあると思います。それらをそれぞれ、work_old および report_old と名前を変えましょう。その後、新規に report および work フォルダを作成します。
実際に work というフォルダーを作成してもらいました。そして、そのwork フォルダーにこれまで作成したソースファイルとそれをコンパイルしたものを移動してもらいました。こんなことをして、ターミナルでの作業(コンパイルおよび実行)には影響ないのでしょうか?(当然影響があります。)
ターミナルを開きます。まえにやったように、
cglsc 0419-1.c
としてみましょう。フォルダー作成等の作業がうまくいっていれば、エラーがでます。なぜなら、コンパイルするべきファイル 0419-1.c を別の場所である work フォルダに移動してしまったからです。
ターミナルを起動した時点では、自分はホームディレクトリと呼ばれる位置にいます(ディレクトリとフォルダーは同じものだと思ってください)。それは、起動時のファイルマネージャーも同様で、起動時にはホームディレクトリの内容を表示しています。先ほどの作業で、ホームディレクトリにあったファイルを workフォルダーにファイルを移動してしまったため、ターミナルを起動した後、
cglsc 0419-1.c
としても、0419-1.c というファイルが見つからないのでエラーとなったわけです(エラーメッセージもファイルが見つからないといったものだったはずです)。正しくコンパイルするためには、work フォルダー内に自分が移動する必要があります。それには、ターミナルで次のコマンドを実行します。
cd work
この新たに出てきたコマンド cd は Change Directory の略で、文字通り自分の位置を変更します。上記コマンドで、work フォルダーの中に移動できたので、改めて
cglsc 0419-1.c
としてみましょう。今度はうまくいくはずです。ついでに、コンパイルされたプログラムが実行できるかどうかも確かめておきましょう。
./0419-1
正しく実行できたと思います。
ところで、ターミナル上で、そのフォルダー内のファイルの一覧を見たい場合もあるでしょう。次のコマンドで見ることができます(ls は LiSt の略です)。
ls -l
ファイル名と、そのサイズ、変更日時などが一覧として表示されます。
さて、今 work フォルダーの中にいますが、先のホームディレクトリに戻るにはどうするのか?次のコマンドで、ホームディレクトリに戻れます。
cd
当面はこれだけのことができれば十分でしょう。実際ターミナル上でもフォルダーを作成することができるのですが、この演習ではフォルダーの作成、ファイルの移動、ファイルのコピーはファイルマネージャーで行うことにします。(Windows や Macintosh を使いなれた人は何も問題ないでしょう)
ターミナルで使えるフォルダーやファイル操作のコマンドのより詳しい情報はこちらにあります。
今後、この演習で作成するファイルは全て work フォルダーに保存するようにしてください。ただし、自動回収によるレポート提出をする場合には、対象となるファイルを report フォルダーにコピーしてもらう必要があります。(計算数学演習と同じ形式です。)
今日は、計算数理Aの講義に出てきた次の常微分方程式を用いて演習を進めます。この方程式は、講義で詳しく説明されたと思いますが、例えば放射性同位体の崩壊を記述するモデル方程式として導出されます。講義で紹介があったように、例えば放射性炭素による年代測定にはこういった微分方程式が役立ちます。N(t) を時刻 t における放射性同位体の原子数とすると下記のような微分方程式が得られることは講義で見たとおりです。
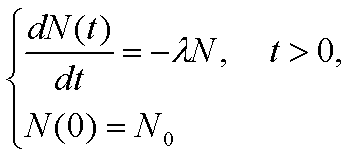 (P)
(P)
さて、この微分方程式は簡単に解けて、解は次のようになることも講義で見ました。
![]() (S)
(S)
今日の目標は、解(S)をグラフとして表示するGLSCプログラムを作成することです。パラメータλおよびN0を与えれば、(S)のグラフをかけるはずです。実は前回の内容で y = sin(x) のグラフを描いてもらいましたが、そこで注意したようにコンピュータを用いてこのようなグラフを描く場合には折れ線近似で描く必要があります。前回の y = sin(x) を描く方法を記述した部分にしたがって、(S)のグラフを描いてください。
課題1
GLSCを用いて、
![]()
のグラフを描け。ただし、
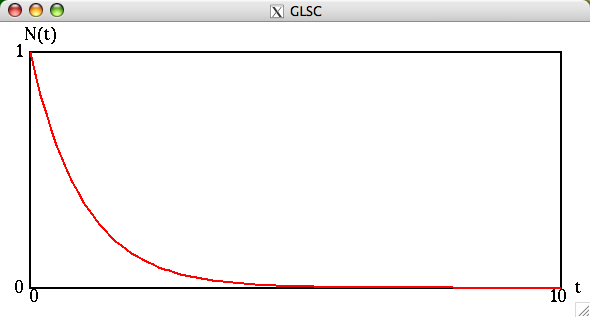
N0=1, λ=1, 0≦t≦10
とする。例えば次のようになる。(この例では、0≦t≦10 を 100等分している。つまり時間刻み幅を dt と書くことにすると、 dt = 10.0/100.0 = 0.1 である。曲線を100本の直線のつながりである折れ線で近似するのである。)
C言語では,ea は exp(a) で求まる.
課題2
N0=1, λ=1のとき,N(τ) = 0.5 となる τ を求めよ。((S)を用いて具体的に求めよ)
答え: log2 (約 0.693)
C言語では log2 は log(2.0)で求まる.
課題3
課題1で作成したプログラムを用いて課題2のτを近似的に次のような手法で求めたい。そのようなプログラムを作成せよ。
方法
N(t) の値を(S)を用いて飛び飛びの t の値 ti = dt*i (ただし dt は時間刻み幅)について求めるのであるが、(S)と課題1のグラフから明らかなように N(t) は単調減少関数である。であるから、
N(ti) > 0.5 ≧ N(ti+1)
となる i がただ一つあるであろう。このとき、 ti を τ の近似値 τ* とする。
小問1:τ* を求めよ.
小問2:
0≦t≦10 を 100等分して上記方法にてτ* を求め、課題2で求めた値との差(誤差と呼ぶ)
err* = |τ- τ*|
を求めよ。
注意:当然ながら刻み数を 100 から 1000 に増やせばより正確な値が求まる。
小問3:
err* は刻み数を変更するとどのようにかわるか?刻み数100, 1000,10000に関してそれぞれ調べ,横軸を刻み数,縦軸をその刻み数に対するerr* として,グラフにしてみよ(gnuplot を用いる).
課題4
課題3の方法ではあまり良い精度で近似値を求めることができない。次の方法でより精度良く近似値をもとめることを考える。課題3と同様に,
N(ti) > 0.5 ≧ N(ti+1)
なる i を求め、2点 (ti, N(ti)), (ti+1, N(ti+1)) を結ぶ直線を考える(下図の青丸および青線).その直線と N = 0.5 の直線の交点の t の値 τ** をもって、τ の近似値をする(下図赤丸).このような手法を線形補間と呼ぶ.下図において,黒い曲線がN(t)であって,黄緑色の丸がτである(ただし,N(t)はわかりやすいように強調して描いてある).
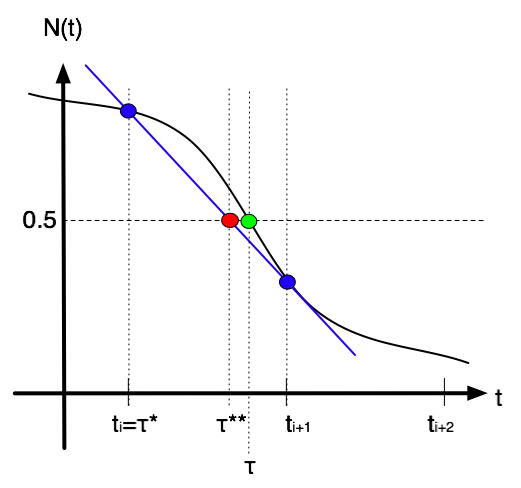
小問1:τ** を求めよ.
小問2:
0≦t≦10 を 100等分して上記方法にて τ** を求め、課題2で求めた値との差
err** = |τ- τ**|
を求めよ。課題3の結果よりも良いだろうか?
注意:
課題3の方法でも刻み数を増やせばより正確な値が求まるのであるが、課題4の補間を使えば、あまり多くない刻み数でも正確な近似値が得られることを実感してほしい。
小問3:
err**は刻み数を変更するとどのようにかわるか?刻み数100, 1000,10000に関してそれぞれ調べ,横軸を刻み数,縦軸をその刻み数に対するerr**として,グラフにしてみよ(gnuplot を用いる).
小問4:
課題3の小問3および,課題4の小問3にて得られたグラフを重ねて表示してみよ(gnuplot を用いる).
課題5
課題4において刻み数100で近似値を求めた場合の誤差と同程度に小さい誤差とするためには課題3において刻み数をどの程度にしなければならないか。実験してみよ。
注意:
課題3、課題4の方法は、 N(t) が具体的に関数として与えられていない場合(例えば実測データなど)にも有効であることに注意。
レポート課題
GLSCを用いて、
![]()
のグラフを描け。ただし、
N0=1, λ=1, 0≦t≦10
とする。次に作成したプログラムの実行例を示す。(この例では、 0≦t≦10 を 100等分している。つまり時間刻み幅を dt と書くことにすると、 dt = 10.0/100.0 = 0.1 である。曲線を100本の直線のつながりである折れ線で近似するのである。)この例の出力に近くなるよう作成すること。課題3または課題4の内容を組み込んだプログラムであって、τの近似値を表示するプログラムであればなお良い。

課題3または課題4の内容を組み込んだプログラムであって、τの近似値を表示するプログラムであればなお良い。例えば次のよう。
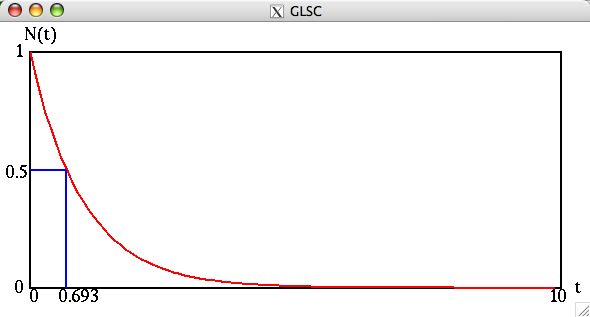
ファイル名は rep0510.c として、report フォルダ内におくこと。なお、ファイルの先頭にコメント文として、自分の学籍番号と名前を記入し、プログラムの途中にもコメント文として処理の内容を書き込むこと。画面表示だけでなく、ソースファイルも見るのでそのつもりで作成すること。(例えば、課題3、課題4の内容を組み込まず、例えば課題1の結果を用いてグラフとしてのみ上記例と似たようなものを出したとしても評価しない。)
自動回収日時:2006年5月23日(火)午後4時
今回は、微分方程式を数値的に解いたわけではないことに注意してください。解析的にもとまった解(S)をグラフにしたにすぎません。来週は、常微分方程式を数値的に解いてもらい、それをグラフ化してもらいます。(計算数学演習でやった内容の復習になります.)
課題3,課題4の内容の発展的内容として次の問題も考えてみて下さい.
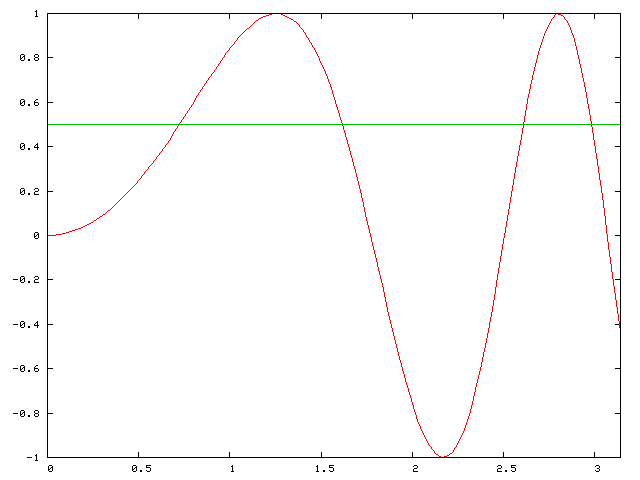
課題3および課題4の方法を用いて,
y = sin(x*x)
と直線
y = 0.5
の交点の x 座標を 0≦x≦πの範囲で全て求めよ.下のグラフに示すように(縦軸をy,横軸をx とした),交点は4つ存在する.