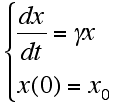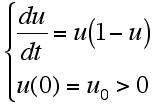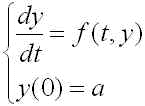 (1)
(1)C言語では、自分で関数を定義し利用することができます。つぎのサンプルプログラムを見てください.
1: #include <stdio.h>
2:
3: int beki(int a, int b);
4:
5: main()
6: {
7: int n;
8:
9: n = beki(2, 3);
10: printf("%d\n", n);
11:
12: printf("%d\n", beki(3, 4));
13: }
14:
15: int beki(int a, int b)
16: {
17: int i, ans;
18:
19: ans = 1;
20:
21: for (i = 1; i <= b; i++)
22: {
23: ans = ans*a;
24: }
25:
26: return ans;
27: }
青字の部分(3行目および15〜27行目)が関数の定義に関わる部分で、赤字の部分(9行目および12行目)で、定義した関数を使用している部分です。まずは定義している部分から見ていきましょう。
3行目: 関数のプロトタイプ宣言と呼ばれる宣言です。後に定義する関数の戻り値の型と、引数の型を仕様として、プログラムの先頭部分(main 関数より前)にこのように書きます。関数を定義する場合には、このプロトタイプ宣言が必ず必要だと思っておいてください。(省略する方法もありますが、この演習では必ずプロトタイプ宣言をすることとします。)
5〜13行目: main 関数の定義です。
15〜27行目: beki 関数の定義です。
y = sin(x)
と書いたとき、sin が関数名で x が関数 sin の引数。変数 y には sin(x) の戻り値が入ることになります。当然変数 x, y にはそれぞれ型があり、関数自体がもつ値(戻り値)にも型があります。
先のサンプルプログラムの3行目のプロトタイプ宣言や、15行目の関数定義の部分で、 int と整数型が宣言されているのはその為です。
では、beki 関数の定義部分を詳しく見ましょう。15行目を見ると
int beki (int a, int b)
となっています。これは、先のプロトタイプ宣言と通常おなじ記述となります。はじめの int は、 beki 関数の戻り値の型が int であるという意味です。続いて関数名 beki があり、その後括弧に囲まれ、2つの変数が定義されています。これらは、引数として渡される値を格納する為の変数でそれらの名前をそれぞれ a, b とし、型はそれぞれ整数型としています。つまり、 beki(1,2) とこの関数が呼ばれた場合、 a には 1 が、 b には 2 が代入されることになります。
つづいて、中括弧に囲まれた、関数本体の処理内容が続きます。この中で、新たに(この関数の定義内でのみ有効な)変数 i と ans を用意しています。さらには、先の引数部分にあった、変数 a, b が参照されています。もちろん、 a, b には関数が呼ばれた時に引数として渡されている変数の内容である数値または直接数値として渡された場合にはその数値が代入されています。
最後の return 文により、 ans の内容が beki 関数の戻り値として返されます。
以上、関数を作る場合に必要なことをまとめると
他の例を見てみましょう。
例えば、実数値の絶対値を表示するプログラムを考えましょう。次のようになります.
#include <stdio.h>
float myabs(float f);
main()
{
float a;
printf("実数を入力してください:");
scanf("%f", &a);
printf("入力された実数の絶対値は %f です。\n", myabs(a));
}
float myabs(float f)
{
if(f < 0.0)
{
f = -f;
}
return f;
}
以前にも述べたように、自分で関数を作る場合には自由な名前をつけることができます。しかし、標準関数として既にある関数の名前をつけることはできません(例えば、printf や scanf といった関数を新たにつくることはできません)。実は絶対値を求める標準関数 abs がありますので、今回は myabs という名前にしています。また、関数の名前も変数の名前の規則同様使える文字と使えない文字があります。注意してください。数字から始まらない英数字を関数名としてください。
#define 文を使うと定数を定義することができます。通常、#include 文の後に書きます。例えば、
#define N (5)
と書いた場合、後のプログラム中の N は全て (5) に置き換わります。例えば、次のように使えます。
#include <stdio.h>
#define A (5)
#define PI (3.1415926)
main()
{
printf("%d, %f\n", A, PI);
}
#define 文は、実は単に文字列を置き換えるだけです。つまり、printf 関数部分に A および PI がありますが、それらはコンパイル時に次のように書き換えられます。
printf("%d, %f\n", (5), (3.1415926));
#define 文を上手に使うと、プラグラムが大変見通しのよいものとなります。
GLSCにおいて使われる定数(G_STOP, G_RED, G_BOTH 等)は、すべて#define 文を用いて宣言された定数です。
C言語では三角関数等の数学関数を用いることができます。数学関数を用いる場合には、
#include <math.h> をプログラムの先頭付近に書き入れることと、コンパイル時に、ファイル名を sample.c とすると、
cc sample.c -o sample -lm
というふうに、最後に -lm を付け足す必要があります。ただし、cglsc コマンドを用いてGLSCを用いたC言語のソースプログラムをコンパイルするときには -lm は自動的につけられた形でコンパイルされるので、付ける必要はありません(付けるとエラーになります)。三角関数を用いた例を次に示します。
#include <math.h>
#include <stdio.h>
#define PI (3.1415926)
#define N (10)
main()
{
int i;
float dtheta;
dtheta = 2*PI/(N-1);
for(i = 0; i < N; i++)
{
printf("%f %f\n", i*dtheta, sin(i*dtheta));
}
}
#define 文の使い方にも注目してください。このように定数としてNを定義しておけば、Nの定義を変更するだけですみ、他の部分の変更は必要ありません。
注意:cglsc コマンドでコンパイルする場合には, -lm は自動的に付け足された形でコンパイルされるので,#include <math.h> のみ気をつければ良い.
C言語では,大域変数を用いる事ができます.次の例を見てください.この例では,実数型変数 A が大域変数とよばれます.main 関数の外(プログラムの先頭付近)で定義されている事に注意してください.この位置で定義すると,そのプログラム中の他の関数定義の中でもその変数を用いる事ができます.下の例では,関数 main の中で A の値を設定し,関数 f の中で A を表示しています.対して,変数 B は局所変数とよばれます.両者の違いは以下のプログラムの動作をみれば分かると思います(一度に多くの事を説明する為の例なので少し分かりにくいかもしれません.実行結果とソースプログラムをよく見比べ,動作を確認してください).大域変数を用いた方がプログラムがすっきりする場合にはつかうと良いでしょう.大域変数とは,そのプログラム中で大域的に使えるという意味であり,局所変数は関数内のみで使えるという意味であると覚えればよいでしょう.
#include <stdio.h>
#include <math.h>
float f(float B);
float A;
main()
{
float B;
A = 1.3;
B = 1.5;
printf("a: %f\n", f(B));
printf("b: %f %f\n", A, B);
}
float f(float B)
{
printf("c: %f %f\n", A, B);
A = 2.0;
B = 1.0;
printf("d: %f %f\n", A, B);
return (B);
}
このプログラムを実行すると以下のような出力が得られる.
c: 1.300000 1.500000
d: 2.000000 1.000000
a: 1.000000
b: 2.000000 1.500000
次のような常微分方程式の初期値問題を、オイラー法と呼ばれる方法を用いて数値的に解き、GLSCを用いて結果をグラフにしてもらいます。オイラー法に関しては,計算数学演習で扱いました.次の問題を考えます。
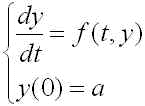 (1)
(1)
求めたいのは、t>0の範囲のy(t)であり、関数 f(t, y) および定数 a は与えられているとします。また、 f(t ,y) の値は t, y が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
コンピューターでは数値を離散的に(とびとびに)しか扱うことができません。そこで、(1)式をコンピューターで扱えるようにする必要があります。(1)をコンピュータで解く方法には色々とありますが、この演習では代表的なオイラー法を用います。その前に、準備として差分商について説明します。
f(x) を x の関数としたとき、f(x) の x=a における微分係数は
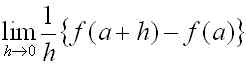 (2)
(2)
で定義されます。ここで、定義中の極限操作を取り払い、h を有限にとどめた
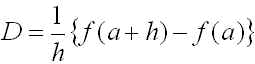 (3)
(3)
を考えると、h を十分小さな正の実数ととれば、(3)式は(2)式の近似となっていると考えられます。この D のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます。いまの場合は1階微分係数を近似する1階差分商です。
では、このような差分商を用いて(1)式を離散化してみましょう。まず、(1)式の第一式の微分係数を上記の差分商で置き換えてみます。
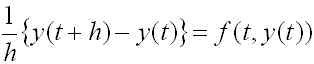 (4)
(4)
ただし、h は正の数とします。(4)式と(1)式の第一式は異なる方程式なので、(1)式の第一式の解 y(t) は一般に(4)式を満たしません。そこで、混乱を防ぐために(4)式の y(t) を Y(t) と書き換えましょう。
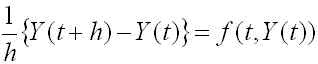 (5)
(5)
(5)式のように差分を含む方程式を差分方程式といいます。
次に、(1)式の y を Y に置き換えた初期条件
![]() (6)
(6)
の下で(5)式を解くことを考えます。(5)式は、
![]() (7)
(7)
と変形できるので、t = 0 を代入すると、
![]() (8)
(8)
となり、Y(0) から直ちに Y(h) が求まります。同様にして(7)式を繰り返し用いると、
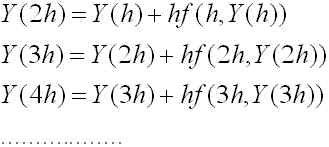 (9)
(9)
というように、j=1,2,3,.... とすると Y((j+1)h) を Y(jh) から計算できることがわかります。
h をいったん決めると、 t=jh 以外の時刻の Y の値は(7)式からは求めることができません。このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。そのようなとびとびの時刻を格子点と呼びます。Y は格子点でのみ意味があるので、そのことを明示するために Y(jh) を Yj と書き換え、 Tj = jh とすると、(5)式と初期条件は、
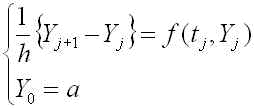 (10)
(10)
となり、結局(1)式の常微分方程式の初期値問題が、Yjに関する漸化式の問題(10)式に置き換えられました。この方法をオイラー法と呼びます。見やすいように(10)を書き直すと(11)になります.
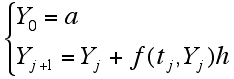 (11)
(11)
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。
T, h, a 及び 関数 f は実数型(float)
N, j は整数型(int)
Y[N+1], t[N+1] は実数型配列(float)
T,Nを設定 (#define文で定数として定義すれば良い)
配列 Y[N+1], t[N+1] を用意する
h = T/N(TおよびN双方が整数型でないか注意)
a の入力を受ける (printf 関数 + scanf 関数)
Y[0] = a (初期値の設定)
t[0] = 0
j = 0,1,2,.......,N-1 の順に (for 文)
t[j+1] = (j+1)*h
Y[j+1] = Y[j] + h*f(t[j], Y[j])
以上を繰り返す
点(t[0], Y[0]), (t[1], Y[1]), ... , (t[N], Y[N]) を直線で結ぶことにより数値解をグラフとして描画 (g_move, g_plot 関数)
オイラー法のアルゴリズム1では,先週や先々週のグラフの描画の仕方にならったアルゴリズムですが,実際には配列を用意する必要はなく,以下のオイラー法のアルゴリズム2で十分です.アルゴリズム2では,数値解を求めながらグラフを描いています.(アルゴリズム1では,数値解を全て求めた後グラフを描いている.)
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。
T, h, a, Y, t 及び 関数 f は実数型(float)
N, j は整数型(int)
T,Nを設定
h = T/N
a の入力を受ける (printf 関数 + scanf 関数)
Y = a
t = 0 でのグラフの描画 (g_move 関数)
j = 0,1,2,.......,N-1 の順に (for 文)
t = j*h
Y = Y + h*f(t, Y)
一定間隔毎にグラフを描画 (g_plot 関数)
(求まった Y は時刻 t+h での値であることに注意)
以上を繰り返す
さて,実際にオイラー法をつかって常微分方程式を解いてみましょう.
今回も、計算数理Aの講義に出てきた次の常微分方程式を用いて演習を進めます。(ただし N を y と書き換えた.上記アルゴリズム等の分割数 N とまぎらわしいので.)
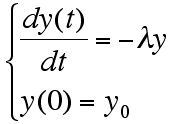 (P)
(P)
前回は,この微分方程式を解析的に解き,得られた解をグラフ化してもらいましたが,今回は(P)をオイラー法を用いて数値計算で解いてもらい,得られた数値解をグラフ化してもらいます.
以下の課題では,できればアルゴリズム2を用いて欲しいが,分かりにくい人はアルゴリズム1を用いても良い.
課題1
(P)をオイラー法で解き,得られた数値解をグラフとして表示するプログラムを作成せよ.ただし,
Y0=1, λ=1, 0≦t≦10
とする。例えば次のようになる。(この例では、0≦t≦10 を 100等分している。つまり時間刻み幅を h と書くことにすると、 h = 10.0/100.0 = 0.1 である。)(縦軸がN(t)となっているがy(t)と読み替えてください.)
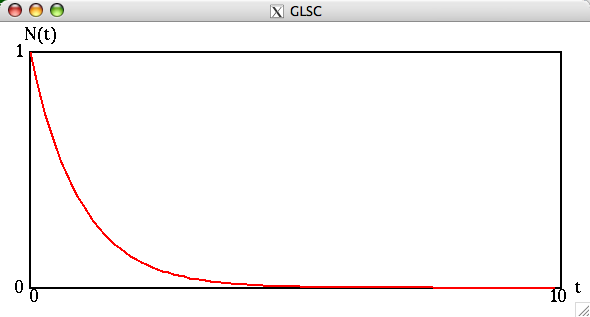
先週,解析的に求めた解をグラフとして表示したものは以下であるが,殆ど違いがない事に注意.(課題2でみるが,微妙に異なっている)
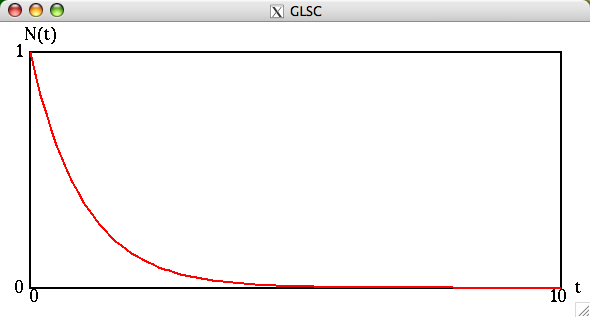
課題2
解析的に求めた解(S)とオイラー法で求めた数値解を重ねて描くプログラムを作成せよ.例えば,次のようになる.この例では,解(S)を緑色で描き,数値解を赤色で描いている.(この例では、0≦t≦10 を 100等分している)
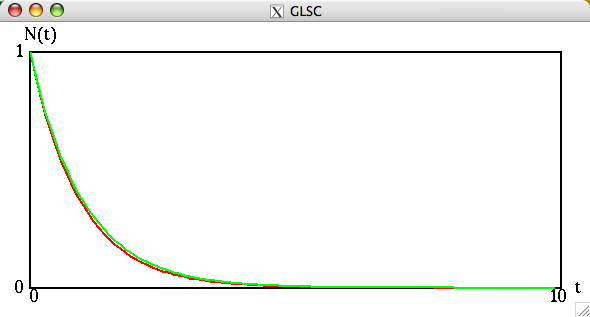
刻み幅を小さくすると両者の差は縮まる.(次の例では、0≦t≦10 を 300等分している)
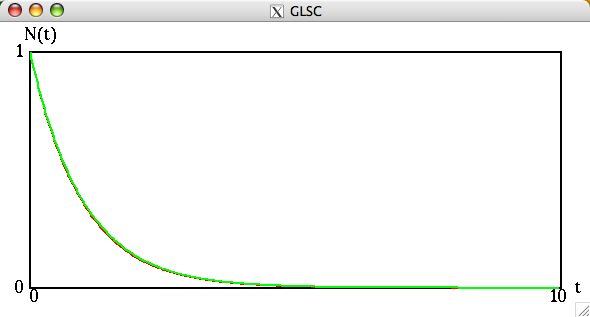
レポート課題
課題2で作成したプログラムを rep0517.c というファイル名で report フォルダにおけ.例えば次のような出力がえられる.0≦t≦10 を 100等分とすること.

自動回収日時:2006年5月30日(火)午後4時