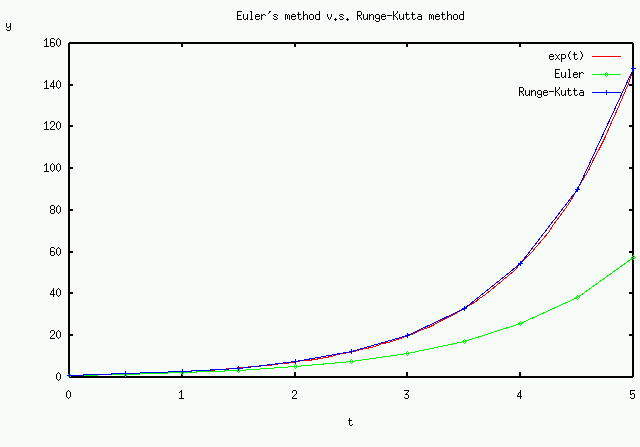
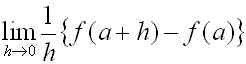(A)今日は以下の内容で演習を行います．
前回，
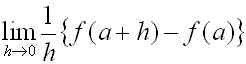(A)
を，
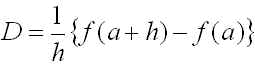(B)
と近似したのだけれども，どの程度の近似になっているのか調べてみよう．（今日の課題３と関係する内容）
テイラーの公式により，
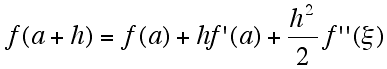
となる．ξは a と a+h の間の数である．これを，(B)に代入し，整理すると，
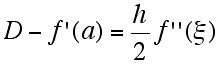(C)
が得られる．右辺は D と f'(a) の差すなわち誤差を与える．f''(x) の値は x=a 付近で有限であるとすると，ランダウの記号を用いて，
(D)
と書ける．この式（(D)式の意味がよくわからない人は（C)式を見てもらってもかまわない）は，h が十分小さければ，D と f'(a) の差，すなわち誤差はせいぜい h に比例して小さくなることを示している．すなわち，オイラー法では，h を小さくすればその小さくした分に比例して真の解に近い近似解が得られるということである．（ただし，コンピュータでは有限桁数の計算しかできない為，上記の議論通りにならない場合がある．h を徐々に小さくしていくと誤差が拡大するということもあり得る．）
２階常微分方程式もオイラー法を用いて解くことができます。これらは計算数学演習でやった内容なので，簡単に紹介するにとどめます．次の問題を考えます（一般的な設定ではなく実例を挙げる事にします）。
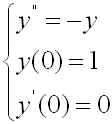（１）
講義にて説明があったはずですが、これは単振動を記述する２階の常微分方程式です。ただし簡単の為、時間 t での微分を ' を用いてあらわしています。２階の常微分方程式は次のように連立の１階の常微分方程式に帰着できます。y1(t)=y(t), y2(t)=y'(t) とおくと、（１）式は，
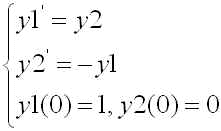（２）
となります。こうなれば、前回紹介したオイラー法を用いて解を求めることができます。アルゴリズムは次のようになります。但し、 T を解を求める時間の上限とし、h を時間刻み幅、N を時間刻み数とします。また、変数は y1, y2 として、a1, a2 を初期値とします。また、f1(t, y1, y2) および f2(t, y1, y2) はそれぞれ関数で（２）式の場合には f1 が第一式の右辺、 f2 が第二式の右辺となります。
課題０
（１）を解け．
解答：y(t)=cos t
オイラー法のアルゴリズム
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。
T, h, a1, a2, y1, y2, y1_new, y2_new, t 及び 関数 f1, f2 は実数型(float)
N, j は整数型(int)
T,N,h を定める
y1 = a1, y2 = a2
t = 0 でのグラフの描画 (g_move 関数)
j = 0,1,2,....,N-1の順に
t = j*h
y1_new = y1 + h*f1(t, y1, y2)
y2_new = y2 + h*f2(t, y1, y2)
y1 = y1_new
y2 = y2_new
一定間隔毎にグラフを描画
(g_plot 関数)
（ここで求まったy1,y2 は時刻t+hのものであることに注意）
を繰り返す
課題１
(2) をオイラー法で解き、グラフを描け。グラフは横軸が t であり、縦軸を y(t) とせよ。また、時間刻み幅 h を変えたときに結果がどのようにかわるか観察せよ。0≦t≦20の範囲において、h=0.0001,0.001, 0.01, 0.1それぞれの場合につい解 y(t)=cos t とどの程度あっているか各自調べよ。
色々な h に対する計算結果は次のようになる（これはＧＬＳＣの出力ではないが、ＧＬＳＣでもおなじようなグラフが作成できる）。この結果から、h は十分小さい値でないとまずいことがよく分かるだろう。
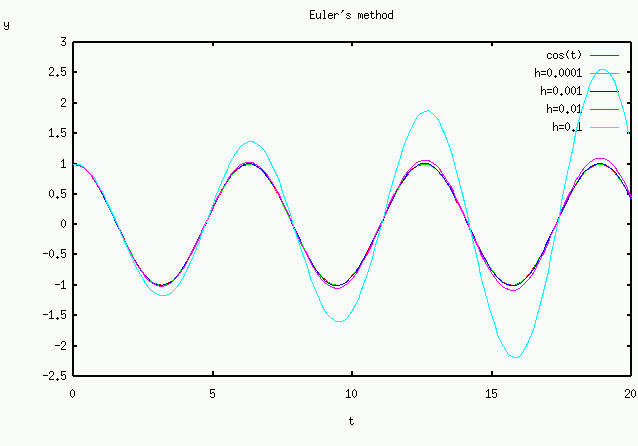
上の課題の結果から分かるように、オイラー法では h を十分小さくとらないと本当の解をうまく近似できません。h を小さく取るということは、計算時間が多くかかることを意味します。そこでより高精度で大きな h でもうまく解を近似できるような解法が求められます。そのような要求に応える解法としてはルンゲ・クッタ法があります。ルンゲ・クッタ法は計算数学演習でもやりました．今日のページの後半にルンゲ・クッタ法に関する説明等があります．
課題２
下の図のように、壁に一端を固定されたバネの他端におもりがつけられている状況を考えます。
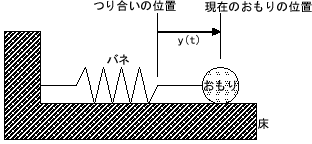
このおもりを少しだけ右に引っ張ってから手をはなす。おもりの中心の時刻 t におけるつり合いの位置からのずれを y(t) とします。また、時刻 0 でのおもりの位置を y(0)=1、おもりの速度を y'(0)=0 とすると、課題２と全く同じ、つぎの単振動の問題となります。
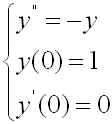（３）
これではおもりに働く力はバネの復元力のみで、ある意味非現実的です。今回は復元力以外におもりの速度 y' に比例する抵抗が働く場合を考えましょう（おもりと床との間の摩擦力のようなものをイメージ）。改良されたモデルは次のようになります(2ky' の項が新たに加わったもので、摩擦のようなものをあらわしている)。
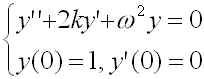（４）
ここで k,ω はそれぞれ抵抗力、復元力の強さを表す正の定数です。課題は、（４）式の問題を連立１階常微分方程式に変換し、オイラー法を用いて解き、ＧＬＳＣをつかってグラフにしてください。k < ω でのグラフと k > ω でのグラフを見比べて違いに関して考察してみて下さい。h を色々と変化させると数値解はどう変化するか？
課題３
以下の課題１で得られたグラフを検討する。
h を小さくすればするほど真の解に近いように見える。真の解と近似解の差が h とどういう関係にあるのかを知りたい。
今、時間刻み幅が h であるときにオイラー法によって得られた近似解を Y(t;h) とすると、t = 1 における真の解と近似解の差の絶対値をもって近似解がどの程度真の解に近いかを判断することにしよう。つまり、
E(h) = | cos(1) - Y(1; h) |
を考える。もしも、近似解が真の解に完全に一致するのであれば、 E は 0 となる。例えば、課題３のように h をそれぞれ、0.1, 0.01, 0.001, 0.0001 と 1/10 になるごとに、E はどの程度小さくなるか調べよ。次のような表を作り、グラフなどを用いて検討すると良い。???の部分を実験して書き込む。オイラー法では、h を 1/10 にすると、E も（大体） 1/10 になるはずである。（このページのはじめにある記述を参照．）
| h | E(h) |
| 0.1 | ??? |
| 0.01 | ??? |
| 0.001 | ??? |
| 0.0001 | ??? |
ここで扱う例のように、時間とともに振動する解をここで示したような方法で比べる場合には注意が必要である。例えば、課題３のグラフを見ればよくわかるが、 t = 5 あたりで比べると、真の解と近似解は一見差がないように見えかつ、h にもよらないように見える。
先週扱った、１階の常微分方程式についても、同様の実験ができる。まずはそちらからやってみるのも良いかもしれない。
以下は，ルンゲ・クッタ法に関する説明です．ルンゲ・クッタ法に関しては計算数学演習でも扱いました．復習的内容ですので，見ておいてください．
オイラー法を用いた数値解法の演習を行いました。オイラー法は単純でそれはそれでよいのですが、実際の解に近い数値解を出すためには、時間刻み幅 h をかなり小さくとらねばならないことが課題の結果からわかりました。そこで、より精度の高い解法が必要となりますが、今回はそのような解法として、ルンゲ・クッタ法を扱い、それを用いた数値解法の演習を行います。
ルンゲ・クッタ法の導出については、このページの最後を参照してください（詳細は参考書を参照してください）。ルンゲ・クッタ法は次にしめすようなアルゴリズムで、オイラー法に比べれば多少複雑なものとなっています（赤字の部分が異なります）。
T を解を求める時間の上限とし、h を時間刻み幅、N を時間刻み数とします。また、変数は y とし、a を初期値とします。r1, r2, r3, r4 はそれぞれ実数型の変数です。
T,N,h を定める
a の入力を受ける (printf 関数 + scanf 関数）
y = a
t = 0 でのグラフの描画 (g_move 関数)
i = 0,1,2,....,Nの順に
t = i*h
r1 = f(t, y)
r2 = f(t + h/2, y + (h/2)*r1)
r3 = f(t + h/2, y + (h/2)*r2)
r4 = f(t + h, y + h*r3)
y_new = y + (h/6)*(r1 + 2*r2 + 2*r3 + r4)
y = y_new
一定間隔毎にグラフを描画 (g_plot 関数)
を繰り返す
課題１
上記のルンゲ ･クッタ法を用いて、次の問題を実際に解き、ルンゲ ･クッタ法がオイラー法と比べてどの程度性能が良いか比べよ。次の初期値問題を 0≦t≦5 の範囲で h=0.5 とし、実際にオイラー法とルンゲ ･クッタ法を用いて解け。
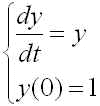
オイラー法を用いた解法プログラムを euler.c とし、同問題をルンゲ ･クッタ法を用いて解くプログラムを rk.c とする。解 y(t) = exp(t) とどの程度あっているか、一目でわかる GLSC プログラムにせよ。
結果は大体次のようになります（このグラフは GLSC でかいたものではありませんが大体同じようなグラフをGLSCで描いてください）。h=0.5とかなり粗く時間刻み幅をとっているにも関わらず、ルンゲ ･クッタ法は良く微分解を近似できていることがわかります。それに比べてオイラー法は微分解から大きく離れてしまっています。これでは正しい計算とは言えないでしょう。
前回の課題で扱った
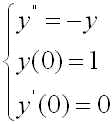（１）
をy1(t)=y(t), y2(t)=y'(t) とおいて次のように連立の１階の常微分方程式に帰着したもの
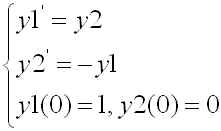（２）
を再び考えます。このような連立の常微分方程式をルンゲ ･クッタ法を用いて解く場合のアルゴリズムを次に示します。ただし、 T を解を求める時間の上限とし、h を時間刻み幅、N を時間刻み数とします。また、変数は y1, y2 とし、それぞれの初期値を a1, a2 とします。r11, r21, r31, r41, r12, r22, r32, r42 および y1_new, y2_new はそれぞれ実数型の変数です。また、f1(t, y1, y2) および f2(t, y1, y2) はそれぞれ実数型の関数で（２）式の場合には f1 が第一式の右辺、 f2 が第二式の右辺となります。
T,N,h を定める
a1, a2 の入力を受ける (printf 関数 + scanf 関数）
y1 = a1
y2 = a2
t = 0 でのグラフの描画 (g_move 関数)
i = 0,1,2,....,Nの順に
t = i*h
r11 = f1(t, y1, y2)
r12 = f2(t, y1, y2)
r21 = f1(t + h/2, y1 + (h/2)*r11, y2 + (h/2)*r12)
r22 = f2(t + h/2, y1 + (h/2)*r11, y2 + (h/2)*r12)
r31 = f1(t + h/2, y1 + (h/2)*r21, y2 + (h/2)*r22)
r32 = f2(t + h/2, y1 + (h/2)*r21, y2 + (h/2)*r22)
r41 = f1(t + h, y1 + h*r31, y2 + h*r32)
r42 = f2(t + h, y1 + h*r31, y2 + h*r32)
y1_new = y1 + (h/6)*(r11 + 2*r21 + 2*r31 + r41)
y2_new = y2 + (h/6)*(r12 + 2*r22 + 2*r32 + r42)
y1 = y1_new
y2 = y2_new
一定間隔毎にグラフを描画 (g_plot 関数)
を繰り返す
課題２
ルンゲ・クッタ法を用いて（２）を解け。前回の課題１，課題3のように、0≦t≦20の範囲において、h=0.0001,0.001, 0.01, 0.1それぞれの場合について解 y(t)=cos(t) とどの程度あっているか各自調べよ。
ルンゲ・クッタ法（今日紹介したものは4段4次のルンゲ・クッタ法とよばれる）では，h を 1/10 にすると，なんと誤差は大体 1/10000 となる．（オイラー法では，h を 1/10 にすると，誤差は大体 1/10 であった．）
アルゴリズムを見れば分かるように，ルンゲ・クッタ法は同じ h を使って計算をした場合に，オイラー法と比較しておおよそ4倍の計算の手間がかかる(関数 f を 4回よび出す事からの概算)．しかしながら，課題2の結果から明らかになったように，例えば，誤差を 1/10000 にしたいという要求が出た場合に，オイラー法であれば，h を 1/10000 にする必要があり，すなわち 10000倍の計算が必要となるが，ルンゲ・クッタ法では， h を 1/10 とするだけで良いので，計算の手間という観点からもルンゲ・クッタ法が有利になる．
常微分方程式の数値計算には，今日紹介した4段4次のルンゲ・クッタ法を用いていればほぼ良い．一部の問題については，他の数値計算法を用いた方が良い場合もあるが，それはその都度参考書を見て対応すればよいでしょう．
課題３
これまでは、横軸を t 、縦軸を y としたグラフを描いてもらいました。例えば横軸を y、縦軸を y' としたグラフを描いてみて下さい。どのようにすればよいでしょうか？またどのようなグラフになりますか？やってみて下さい。
課題４
重力の作用のみを受けて運動する物体を考えます（真空中でボールを投げるような状況）。ニュートンの運動の第二法則から物体の時刻 t での鉛直方向の位置を y(t) とするとその物体の鉛直方向での運動は次のような常微分方程式で表されます。（下向きを正とする）
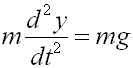（５）
m は物体の質量、g は重力加速度です。色々な初期値 y(0), y'(0) を与えてシミュレーションしてみて下さい。
以下に，いくつかの課題を示しておきます．これら課題を理解する為には，図書館等に行って多少調べごとをする必要があるでしょう．より発展的な内容に興味がある人は是非取り組んで下さい．
課題５（発展的内容：全ての人がする必要はありません．興味がある人はどうぞ．）
さらに、上の問題に空気の抵抗のようなものを加味してみましょう。物体にかかる抵抗がそのときの物体の速度に比例するとすると、運動方程式は、
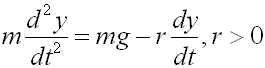（６）
となります。ただし、r は抵抗の強さを表します。色々な初期値および m, r で計算してみてください。空気抵抗を加味する前と様子は変わりましたか？
なお、両問題とも解析的に解ける問題ですので、実際に解いてみて、今回のシミュレーション結果と見比べて理解を深めて下さい。
課題６（発展的内容：全ての人がする必要はありません．興味がある人はどうぞ．）
上の両問題では物体の鉛直方向のみの運動を考えましたが、水平方向の運動も加味するとどのような運動方程式になり、その解はどのようになりますか？運動方程式を立て、シミュレーションしてみて下さい。
課題７（発展的内容：全ての人がする必要はありません．興味がある人はどうぞ．）
惑星の運動を考えます。万有引力の法則から２物体（質量はそれぞれ M,m）に働く力は
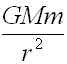
となります。rは２物体間の距離、Gは万有引力定数で
です。原点に太陽（質量 M）があり、惑星（質量 m）の位置を
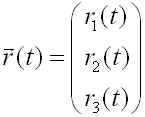
とします。惑星に働く力は
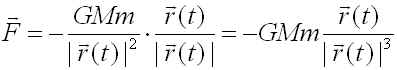
となり、
より
とおくと、２階の常微分方程式の初期値問題
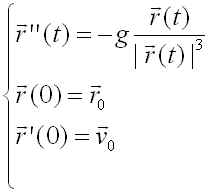
が得られます。これを１階の常微分方程式系に直し、数値計算にて解をもとめて下さい。
課題８（発展的内容：全ての人がする必要はありません．興味がある人はどうぞ．）
１９６０年代初頭に気象学者エドワード・ローレンツは流体力学に基づく次のような単純な３変数系の常微分方程式を示しました。
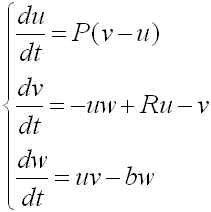
このモデルはいわゆるカオスを生じるモデルとして有名です。パラメータは P, R, b の３種類がありますが、P=16, b = 4, R=35として、u-w平面に解の軌道をプロットすると次のような図ができあがります。（初期値 (u0, v0, w0) = (5, 5, 5), t=0 から t=100 までの計算結果を線でつないだもの）
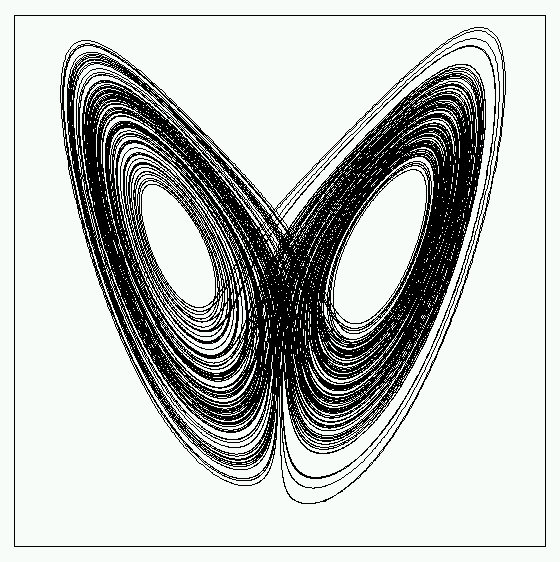
これはストレンジアトラクター（奇妙なアトラクター）と呼ばれるもので、有名なので目にしたことがある人も多いと思います。このようなカオス的な解の挙動が天気予報があたらない理由となっているともいわれています（バタフライ効果という言葉も聞いた事がある人もいるでしょう）。例えば P=16, b=4 として R を色々と変えてみると、解の挙動があれこれ変わります。色々と試してみると面白いでしょう。
ルンゲ・クッタ法について
簡単にルンゲ ･クッタ法について説明します。演習で取り扱ったルンゲ ･クッタ法は４段公式とよばれるものですが、ここでは簡単の為、２段公式を取り扱います。
次の常微分方程式の初期値問題の数値解を求めたいとしましょう。
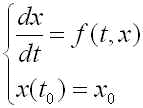（R1）
２段公式とは、 
で（R1）の近似解 
が求められたとして、時間ステップ幅 h だけ進んだ 
における値 
を次の形で計算する公式です。
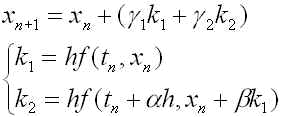（R2）
つまり、からへ進む１ステップにおいて方程式（R1）の第一式の右辺の
を２回計算するので、２段公式と呼びます。この２段公式には、パラメータ 
が含まれますが、これらは方程式（R1）の真の解 x(t) のテイラー展開
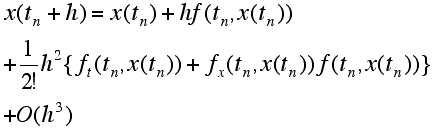（R3）
と（R2）式の第一式の同様の展開とが h のなるべく高い次数の項まで一致するように定めます。つまり、
と仮定して（R2）式の 
の式の右辺を 周りでテイラー展開すると、
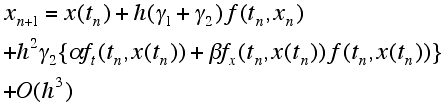（R4）
となります。これと（R3）が
の項まで一致するように
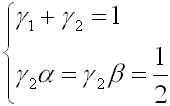（R5）
とおく。公式（R2）で定められる近似解のテイラー展開が h の２次の項まで真の解のテイラー展開に一致するという意味で、この公式を２次の公式と呼びます。この公式は２段公式でもあるので、２段２次の公式とも呼ばれます。パラメータを定める方程式（R5）には自由度が２残っているのでその定め方によって色々な公式が導かれます。（改良オイラー法、ホイン法、修正オイラー法など）
演習で用いた４段４次のルンゲ ･クッタ法の公式も同様にして求めることが出来ます。