数理工学センター
数理工学センターコラム
「物を壊すことなく内部を「見る」には?」
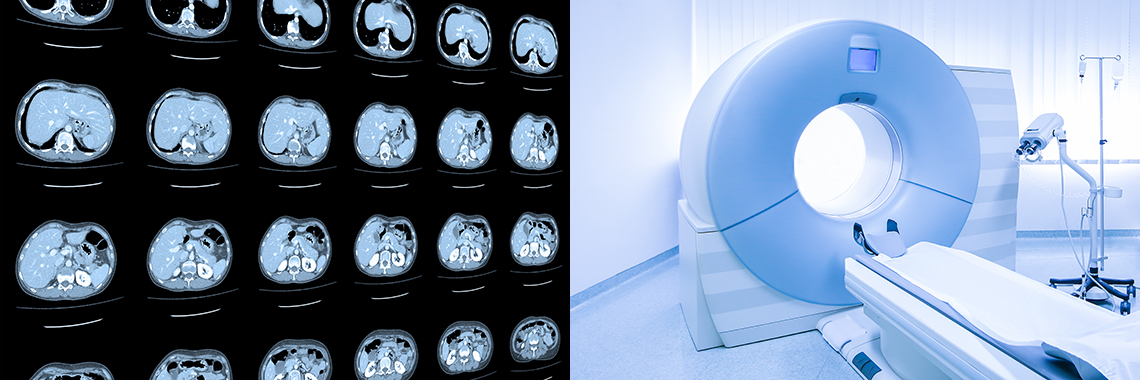
医療診断を行う際には、体の内部の状態を知るための検査が必要ですが、そのために一々手術を行うのでは、医師と患者双方にとって負担や危険が大きくなります。そこで、体の一部を切ったりすることなく内部を観察する方法が用いられます。今日ではその方法には様々なものがありますが、現在でも用いられている代表的なものの一つが、ここで紹介するCT(Computed Tomography、コンピュータ断層撮影)という技術です。
CTの技術も今日では一通りではありませんが、ここでは、最初に実用化されたX線CTについて触れます。このように物を壊すことなく内部を「見る」技術は、医療の場面以外にも、金属部品などの検査(非破壊検査)をする産業の場面でも用いられています。
さて、ここでCTを紹介するのは、もちろんこれが「数理工学」に深く関係しているからです。
体の内部を観察する方法として、おそらく皆さんによりなじみがあるのは、健康診断でも行うレントゲンのX線撮影ではないでしょうか。これも内部を観察する方法の一つですが、レントゲンが一方向のみからのX線照射による像を出力するのに対して、CTは多方向からのX線照射によって得られた複数の像の情報を用いて断面画像を構成し、それを出力するという違いがあります。つまり、CTは単に撮影したものを出力するのではなく、撮影によって得られた情報にある数学的方法を適用してできる画像を出力するのです。また、この数学的方法の適用は、コンピュータを用いた計算によって行われます。
以下ではこの仕組みの概要を紹介したいと思います。なお、CTの実用化に貢献した物理学者コーマック(Cormack)と、レコード会社EMIの技師ハウンズフィールド(Hounsfield)は、1979年にノーベル生理学・医学賞を受賞しています [1]。
数学のどの領域の話か
しかし実は、問題が積分の式で表現されていても、そのままでは断面画像を計算することは困難です。何故なら、現実の複雑な物体を扱う場合、積分計算の結果が数式できれいに書けることは稀だからです。そこで、積分で表現された式をうまく近似して計算ができるようにします。さらに、この近似で導かれた式に基づく計算は、人間の手計算では事実上不可能な大規模な計算になるため、コンピュータの使用が不可欠です。したがって、コンピュータに数学的な計算を実行させるための手法も必要になります。このような近似方法およびコンピュータによる計算方法を研究開発する分野は 数値解析とよばれ、ここで紹介するCTの場合に限らず、様々な分野で様々な方法が考案され、利用されています。
なお、以下で紹介する方法の場合は、近似を行った結果、解くべき方程式として連立一次方程式が現れます。この意味では 線形代数も関連分野と言えます。
以上はCTで用いられる数学的方法の大まかな領域分類でしたが、一方、複数の撮影データから断面画像を構成するという問題は「逆問題」の一種であると言えます。逆問題とは、ごく大雑把にいえば「結果」から「原因」を特定する問題のことです。CTの場合で言えば、これはX線撮影データという「結果」から、物体の断面構造という「原因」を特定する問題であると言えます。逆問題の解析は一つの大きな分野であり、他の代表例として、地震波の観測結果から震源を特定する問題が挙げられます。
数式を用いた解説
写真に使われている数式
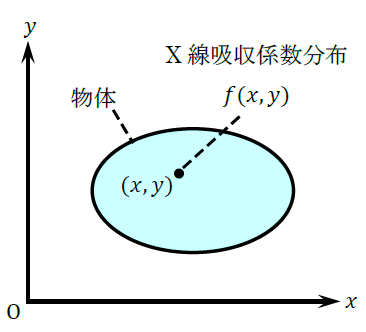
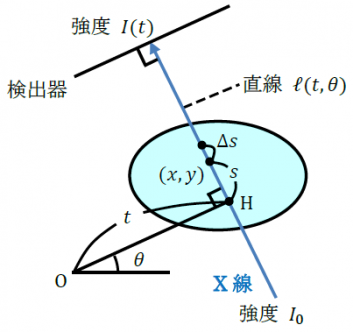
観察対象となる物体の断面が $xy$ 平面上にあるとし、その中の点 $(x,y)$ におけるX線吸収係数の分布を $f(x,y)$とします。 $f(x,y)$ はほぼ通常の物質の密度に比例するので、$f(x,y)$ が分かれば物体の内部構造が分かると考えられます。次に、この物体に、原点からの(符号付き)距離が $t$ で $x$ 軸からのなす角が $\theta$ の方向の法線を持つ直線 $\ell(t,\theta)$ に沿って、$X$ 線を照射するとします(図2)。光源でのX線の強度が $I_0$ であるとき、物体を通過して検出器で観測されるX線の強度 $I(t)$ は、
$ \begin{align} { I(t)=I_{0}\exp\{-P_{f}(\ell(t, \theta))\} } \tag{1}\ \end{align} $
と表されます。ここで
$ \begin{align} { P_{f}(\ell(t,\theta))=\int_{-\infty}^{\infty}f(t\cos\theta -s\sin\theta, t\sin\theta+s\cos\theta)ds } \tag{2}\ \end{align} $
です。よって、実際の観測(撮影)結果から $\log \{ \frac{I(t)}{I_0} \}$ の値を求めることで、各直線 $\ell(t,\theta)$ に対する $P_f(\ell(t,\theta))$ の値が求められます。
式(2)は、与えられた $x$ と $y$ の関数 $f(x,y)$ に対し、$t$ と $\theta$ の関数 $P_f(\ell(t,\theta))$ を定める積分変換を表しています。そこでこの $P_f(\ell(t,\theta))$ を $Rf(t,\theta)=P_f(\ell(t,\theta))$ のような記号で表すと、記号 $R$ は、関数 $f$ に関数 $Rf$ を対応させるという変換 $f \mapsto Rf$ を表します。この変換をラドン変換と呼びます。よって、CTを実現するためには、各 $t$ と $\theta$ に対して(つまり各直線 $\ell(t,\theta)$ に対して)関数値 $Rf(t,\theta)$ が与えられたときに関数 $f$ を求めよ、という問題を解くことになります。
解説
$x=t\cos\theta - s\sin\theta, y=t\sin\theta + s\cos\theta$
となります。点 $(x,y)$ でのX線強度を $I$ とし、これの直線 $\ell(t,\theta)$ に沿った変化を考えます。点 $(x,y)$ から $\ell(t,\theta)$ に沿って微小変位 $\Delta s$ の範囲を通過する際の、X線の強度変化を $\Delta I$ とおくと、
$\displaystyle\frac{\Delta I}{I}=-f(x,y)\Delta s=-f(t\cos\theta - s\sin\theta,\ t\sin\theta+s\cos\theta)\Delta s$
となります。これはランベルトの吸収則と呼ばれます。これを $s$ で積分することで式(1)および(2)が得られます。
さて、前述の問題を解くためには、ラドン変換の逆変換$g \mapsto R^{-1}g$ を求めればよいことになります$(R^{-1}$は、数の-1乗ではなく、逆変換を表す記号です)。この逆変換 $R^{-1}$ を表す式はラドンによって1917年に発見されており、やはりある積分を用いて書けることが知られています。
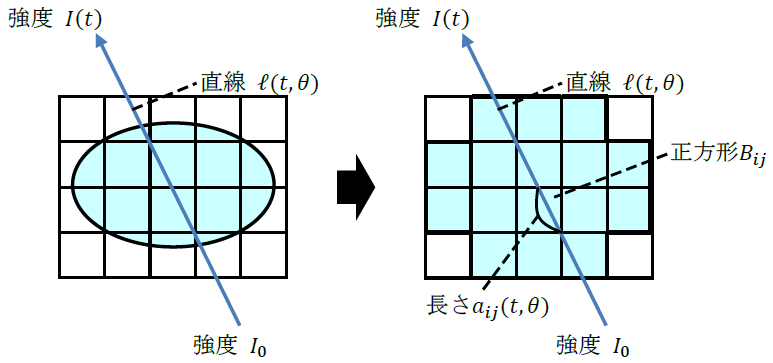
しかし既に述べたように、積分の式をそのまま用いて計算を行うことは殆どの場合に困難です。そこで、式(2)を計算が容易な形で近似することを考えます。ここでは以下に示す図3のように、物体を平面上の等間隔格子で近似し、各格子内ではX線吸収係数の分布 $f(x,y)$ は一定値と見なす近似を行います。式で書けば、各格子の正方形を $B_{ij}$ で表すとき、
$ \begin{align} { f(x,y)\approx\displaystyle\sum_{i,j}f_{ij}\chi_{ij}(x,y) } \tag{3}\ \end{align} $
という近似を考えます($\approx$は近似を表します)。ここで $\chi_{ij}(x,y)$ は
$\chi_{ij}(x,y)=\left\{\begin{array}{l} 1 ((x,y)\in B_{ij})\\ 0 ((x,y)\not\in B_{ij}) \end{array}\right.$
という関数です。格子の間隔を $0$ に近づけていけば、近似の精度は上がっていきます。
式(3)の右辺を式(2)に代入することで
$ \begin{align} { \eqalign{ Rf(\displaystyle t,\theta) &= P_{f}(\ell(t,\theta))\approx\int_{-\infty}^{\infty}\displaystyle\sum_{i,j}f_{ij}\chi_{ij}(t\cos\theta-s\sin\theta, t\sin\theta+s\cos\theta)ds \\ &= \sum_{i,j}f_{ij}\int_{-\infty}^{\infty}\chi_{ij}(t\cos\theta-s\sin\theta,t\sin\theta+s\cos\theta)ds \\ &= \sum_{i,j}f_{ij}a_{ij}(t,\theta) } } \tag{4}\ \end{align} $
という近似が得られます。ここで $a_{ij}(t,\theta)$ は、正方形 $B_{ij}$ が直線 $\ell(t,\theta)$ から切り取る線分の長さです(図3参照)。
さらに、ここまでは任意の $t$ と $\theta$ の組 $(t,\theta)$ について $Rf(t,\theta)$ の値が観測されると考えましたが、実際には、無限個の $(t,\theta)$ についての観測結果を得ることは不可能です。そこで、有限個の $(t,\theta)$ について観測結果が得られるとして、それらを $(t_k,\theta_k )$ $(k=1,…,N)$ とおきます。これらに対して得られた観測値を $c_k=Rf(t_k,\theta_k)$ $(k=1,…,N)$ とおき、さらに式⑷を等式に置き換えた式を考えれば
$ \begin{align} { c_{\kappa}=\displaystyle \sum_{i,j}f_{ij}a_{ij}(t_{k},\theta_{k}) (k=1,\ \ldots,N) } \tag{5}\ \end{align} $
となり、関数 $f$ の近似値 $f_{ij}$ に関する連立一次方程式が得られます。これを解けば関数 $f$ が近似的に求められ、CTが実現されます。しかし実際には、方程式(5)がきちんと解けるものになるにはどのような直線 $\ell(t,\theta)$ を選べば十分かという問題や、実際にコンピューターで方程式(5)の解を計算するにはどのような計算法がよいかという問題など、考えるべき問題は数多くあります。また、今回ここで紹介した方法以外にも、例えばフーリエ(Fourier)解析を用いた方法などもあります。詳細については、参考文献[2]の第1章およびその中の参考文献などを参照してもらえればと思います。
参考文献
http://www.nobelprize.org/nobel_prizes/medicine/laureates/1979/
[2] 若山正人 編:技術に生きる現代数学,岩波書店,東京,2008.

著者
田中 健一郎
中学のときに図形分野(初等幾何)の問題をやり始めたことがきっかけで数学が好きになりました。補助線を引くなどして、問題を既知の基本事項が使える問題に帰着し、きれいに証明を完結させることが面白くてのめり込んでいた記憶があります。高校から大学にかけては、極限という概念によって、無限の対象を有限の手続きで厳密に取り扱うことができることに感銘を受け、解析学分野に興味を持つようになりました。これと同時に、現実世界と結びつく問題に対して具体的な解析をやりたいという動機が、数値解析に興味をもった理由かもしれません。ただ、「なんとなくこれが自分に合っているのではないか」という感覚的な理由も大きいような気がしています。