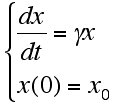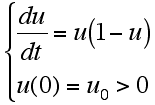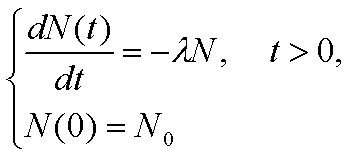 (P)
(P)前回の常微分方程式について。
前回の授業では,次のような常微分方程式を扱いました。
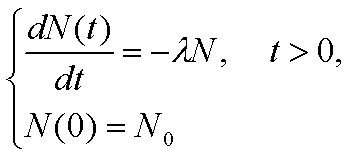 (P)
(P)
また,この常微分方程式の解が次のようになることから,
N(t) = N0 e-λt (S)
このグラフを 0≦t≦10 の範囲で描画し,さらに,
N(τ) = N0/2
となる τ は log2 ですが(τにN0が含まれない事に注目),それを近似的に求めることをしました。さて,この方程式(P)は様々な現象のモデル方程式と見ることができます。先の τ を求める問題との関係から言えば,(P)は放射性炭素・年代測定法との関係を説明するのが適切でしょう。
放射性炭素・年代測定法は,W.F. Libby が 1940年代後半に開発した方法で(1960年にノーベル化学賞を受賞),今世紀初めに英国の実験物理学者ラザフォード等によって発見・開発された放射能の原理に基づくものです。ある種の原子はもともと不安定であるため,外部からの影響が無くとも時間が経つと放射性物質を放射し,他の新しい元素に遷移します。実験結果から,ラザフォードは,放射性物質のいくつかについて,単位時間あたりの元素の崩壊個数は現在の原子数に比例する事を示しました。すなわち,時刻 t におけるある放射性物質中の原子の個数を N(t) とすると,
dN/dt = -λN
が成り立ちます。ここで,λは正の定数で崩壊定数と呼ばれ,物質毎に決まるものです。ある特定の物質のλは実験によって定める必要があります。実際には,実験的に崩壊定数を求めるのではなく,半減期τを測定し,それから崩壊定数λを決めるようです。
時刻 0 における,原子の個数が N0 であるとき,つまり (P) を解けば,
N(t) = N0 e-λt
が解として求まります。したがって, t=τ において,N=N0/2 ならば,
N0/2 = N0 e-λτ
よって,
τ= log2/λ
が分かります(τにN0が含まれない事に注意)。実験的に知られているいくつかのサンプルの半減期を以下に示します。
| 物質 | 半減期 |
| キセノン133 | 5日 |
| バリウム140 | 13日 |
| 鉛210 | 22年 |
| ストロンチューム90 | 25年 |
| 炭素14 | 5568年 |
| プルトニューム | 23103年 |
| ウラン | 4.5×109年 |
放射性炭素・年代測定法においては,炭素14が重要です。これについて,崩壊定数を求めると,
λ = log2/τ = 1.245×10-4 /年
となります。さて,放射性炭素・年代測定法がなぜに成り立つかを少しだけ説明しましょう。
自然界には3種類の炭素があります。それぞれ,炭素12,炭素13,炭素14と呼ばれ,それぞれの存在比率は
炭素12:98.9%
炭素13:1.1%
炭素14:0.00000000012% (おおよそ一兆分の一)
です。また,炭素12,炭素13は安定な物質だが,炭素14は不安定な物質で,時間と共に放射線を放出して窒素14になり,その半減期は,前述の5568年です。
炭素14は,宇宙から降り注ぐ宇宙線によって,窒素14から生じます。生成された炭素14は,生成後直ちに酸素と結合し二酸化炭素として通常の二酸化炭素と共に大気中に拡散します。炭素14の生成速度と,先の崩壊速度がおおむね釣り合っており,その結果大気中の炭素14はほぼ一定と見なすことができることが知られています。
さて,その炭素14を含む二酸化炭素は,光合成によって通常の二酸化炭素と共に植物に取り込まれ,食物連鎖によって動物にも広がります。例えば,木の場合,木が生きている間は二酸化炭素の形で炭素14と他の炭素12,炭素13を吸収し続けるため,木に含まれる炭素14の比率は大気中と同じであると考えられます。つまり,おおよそ一兆分の一の比率で炭素14が含まれているはずです。
その後木が死ぬとどうなるか?例えば,木の加工品を作ろうと人が木を伐採するとそのとき木は死に,光合成の停止と共にあらたな炭素14の取り込みは停止します。その後は,炭素14は,その崩壊速度に従って崩壊するのみとなります。(他の炭素12,炭素13は安定な物質なので崩壊しない。)
この事実から,例えば測定したい木でできた加工品について,精密に炭素14と他の炭素12,炭素13との比率を測定したとして,その比率が例えば二兆分の一であったなら,その加工品はおおよび5500年前のものであることが分かるという理屈です。
前回(第2回(2017年6月20日))の課題3,課題4,課題5について、以下のものをレポートとして期限までにMUSCATを用いて提出しなさい。(レポート課題の提出先は提出課題提出場所と混乱しないよう、来週設置します。)
(注意)
Pythonにおける関数の定義と利用、変数の有効範囲等の説明は、数理工学実験2のここを参照しながら授業中に解説します。先週作成したプログラムを関数を使うもに変更します。
次のような常微分方程式の初期値問題を、オイラー法(Euler method)と呼ばれる方法を用いて数値的に解き、matplotlibを用いて結果をグラフにしてもらいます。教科書の第5章の内容となります。次の問題を考えます。
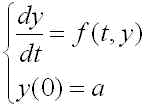 (1)
(1)
求めたいのは、t>0の範囲のy(t)であり、関数 f(t, y) および定数 a は与えられているとします。また、 f(t ,y) の値は t, y が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
コンピューターでは数値を離散的に(とびとびに)しか扱うことができません。そこで、(1)式をコンピューターで扱えるようにする必要があります。(1)をコンピュータで解く方法には色々とありますが、まずは代表的なオイラー法を用います。その前に、準備として差分商について説明します。
f(x) を x の関数としたとき、f(x) の x=a における微分係数は
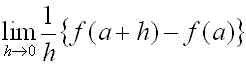 (2)
(2)
で定義されます。ここで、定義中の極限操作を取り払い、h を有限にとどめた
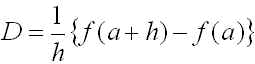 (3)
(3)
を考えると、h を十分小さな正の実数ととれば、(3)式は(2)式の近似となっていると考えられます。この D のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます。いまの場合は1階微分係数を近似する1階差分商です。
では、このような差分商を用いて(1)式を離散化してみましょう。まず、(1)式の第一式の微分係数を上記の差分商で置き換えてみます。
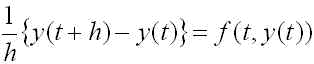 (4)
(4)
ただし、h は正の数とします。(4)式と(1)式の第一式は異なる方程式なので、(1)式の第一式の解 y(t) は一般に(4)式を満たしません。そこで、混乱を防ぐために(4)式の y(t) を Y(t) と書き換えましょう。
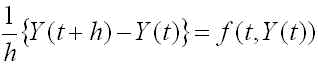 (5)
(5)
(5)式のように差分を含む方程式を差分方程式といいます。
次に、(1)式の y を Y に置き換えた初期条件
![]() (6)
(6)
の下で(5)式を解くことを考えます。(5)式は、
![]() (7)
(7)
と変形できるので、t = 0 を代入すると、
![]() (8)
(8)
となり、Y(0) から直ちに Y(h) が求まります。同様にして(7)式を繰り返し用いると、
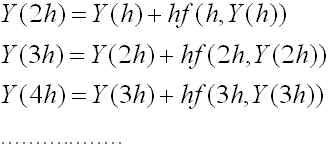 (9)
(9)
というように、j=1,2,3,.... とすると Y((j+1)h) を Y(jh) から計算できることがわかります。
h をいったん決めると、 t=jh 以外の時刻の Y の値は(7)式からは求めることができません。このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。そのようなとびとびの時刻を格子点と呼びます。Y は格子点でのみ意味があるので、そのことを明示するために Y(jh) を Yj と書き換え、 Tj = jh とすると、(5)式と初期条件は、
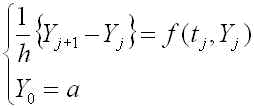 (10)
(10)
となり、結局(1)式の常微分方程式の初期値問題が、Yjに関する漸化式の問題(10)式に置き換えられました。この方法をオイラー法と呼びます。見やすいように(10)を書き直すと(11)になります.
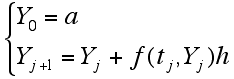 (11)
(11)
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。
T, h, a 及び 関数 f は実数型(float)
N, j は整数型(int)
Y[N+1], t[N+1] は実数型配列(float)
T,Nを設定
配列 Y[N+1], t[N+1] を用意する
h = T/N(TおよびN双方が整数型でないか注意)
a の入力を受ける (print 関数 + input 関数)
Y[0] = a (初期値の設定)
t[0] = 0
j = 0,1,2,.......,N-1 の順に (for 文)
t[j+1] = (j+1)*h
Y[j+1] = Y[j] + h*f(t[j], Y[j])
以上を繰り返す
点(t[0], Y[0]), (t[1], Y[1]), ... , (t[N], Y[N]) を直線で結ぶことにより数値解をグラフとして描画 (matplotlib)
オイラー法のアルゴリズム1は,先週のグラフの描画の仕方にならったアルゴリズムで,計算結果を全て保存しています。しかし、グラフ描画のために全ての計算結果を保管する必要は無く、以下のオイラー法のアルゴリズム2で十分です.
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。また、一定間隔 INTV 毎に計算結果を記憶することとする。
T, h, a, Y, t 及び 関数 f は実数型(float)
N, j は整数型(int)
T,N,INTVを設定
空のリスト Yg, tg を用意する
h = T/N
a の入力を受ける (print 関数 + input 関数)
Y = a
t = 0 での値を記憶(リストに追加)
j = 0,1,2,.......,N-1 の順に (for 文)
t = j*h
Y = Y + h*f(t, Y)
一定間隔(INTV)毎に値を記憶(リスト tg, Yg に追加)
(求まった Y は時刻 t+h での値であることに注意)
以上を繰り返す
点(tg[0], Yg[0]), (tg[1], Yg[1]), ... , (tg[N/INTV], Yg[N/INTV]) を直線で結ぶことにより数値解をグラフとして描画 (matplotlib)
さて,実際にオイラー法をつかって常微分方程式を解いてみましょう.
前回からの常微分方程式を用いて演習を進めます。(ただし N を y と書き換えた.上記アルゴリズム等の分割数 N とまぎらわしいので.)
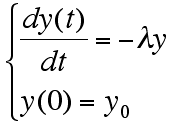 (P)
(P)
前回は,この微分方程式を解析的に解き,得られた解をグラフ化してもらいましたが,今回は(P)をオイラー法を用いて数値計算で解いてもらい,得られた数値解をグラフ化してもらいます(違いを確認).
以下の課題では,できればアルゴリズム2を用いて欲しいが,分かりにくい人はアルゴリズム1を用いても良い.
課題1
(P)をオイラー法で解き,得られた数値解をグラフとして表示するプログラムを作成せよ.ただし,
Y0=1, λ=1, 0≦t≦10
とする。例えば次のようになる。(この例では、0≦t≦10 を 100等分している。つまり時間刻み幅を h と書くことにすると、 h = 10.0/100.0 = 0.1 である。)(縦軸がN(t)となっているがy(t)と読み替えてください.)
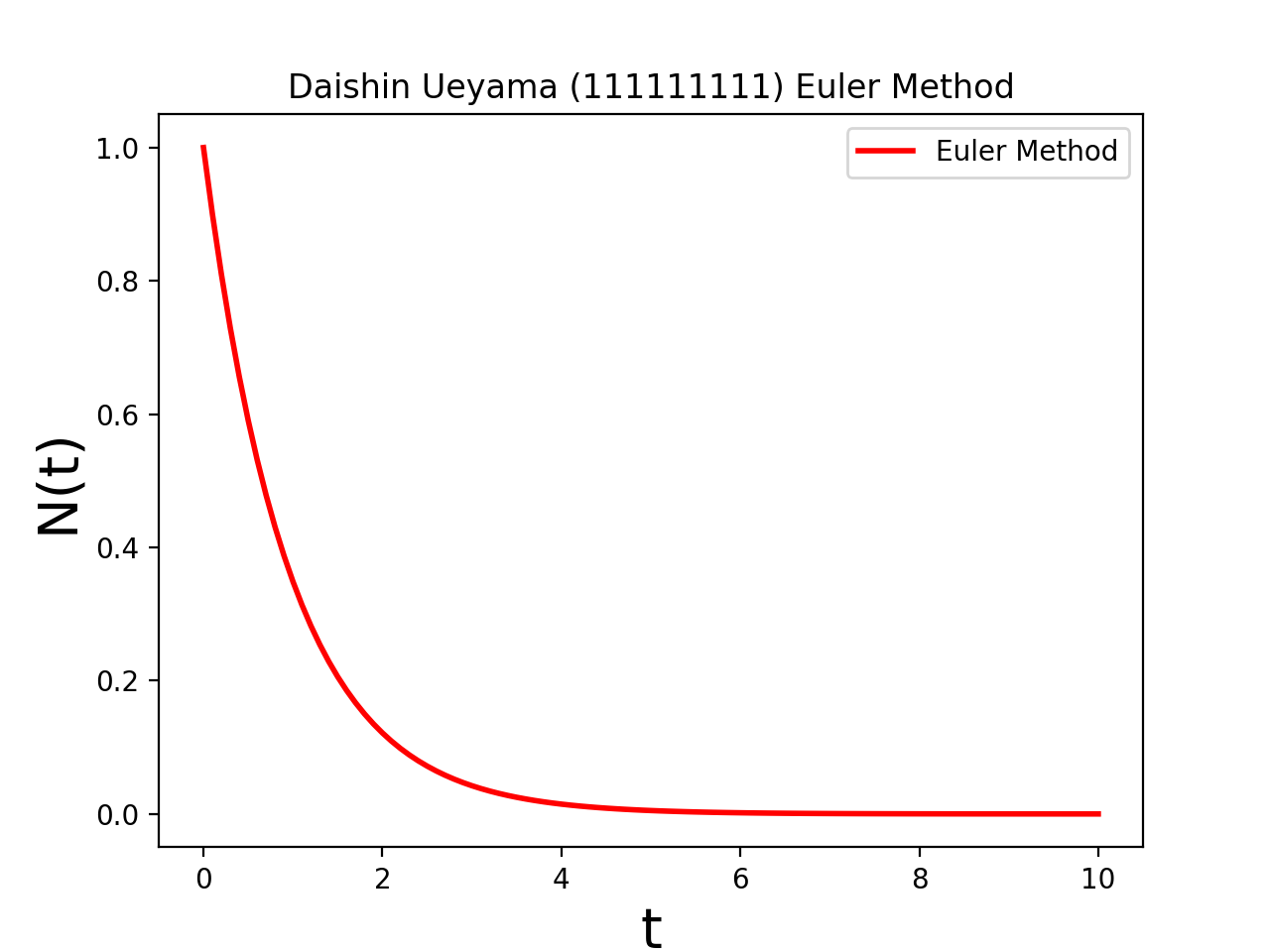
先週,解析的に求めた解をグラフとして表示したものは以下であるが,殆ど違いがない事に注意.(課題2でみるが,微妙に異なっている)
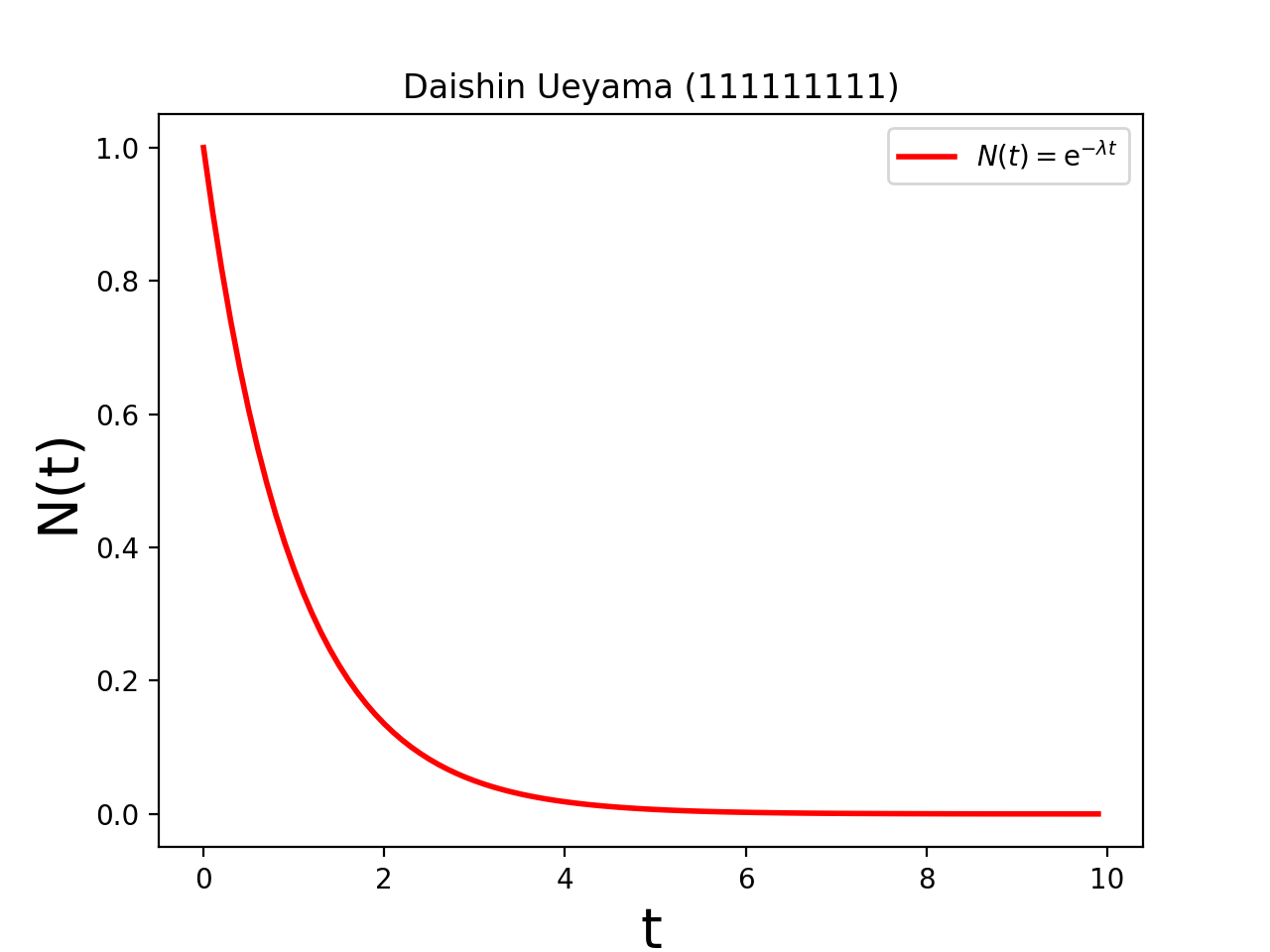
課題2(次回レポート課題になる予定)
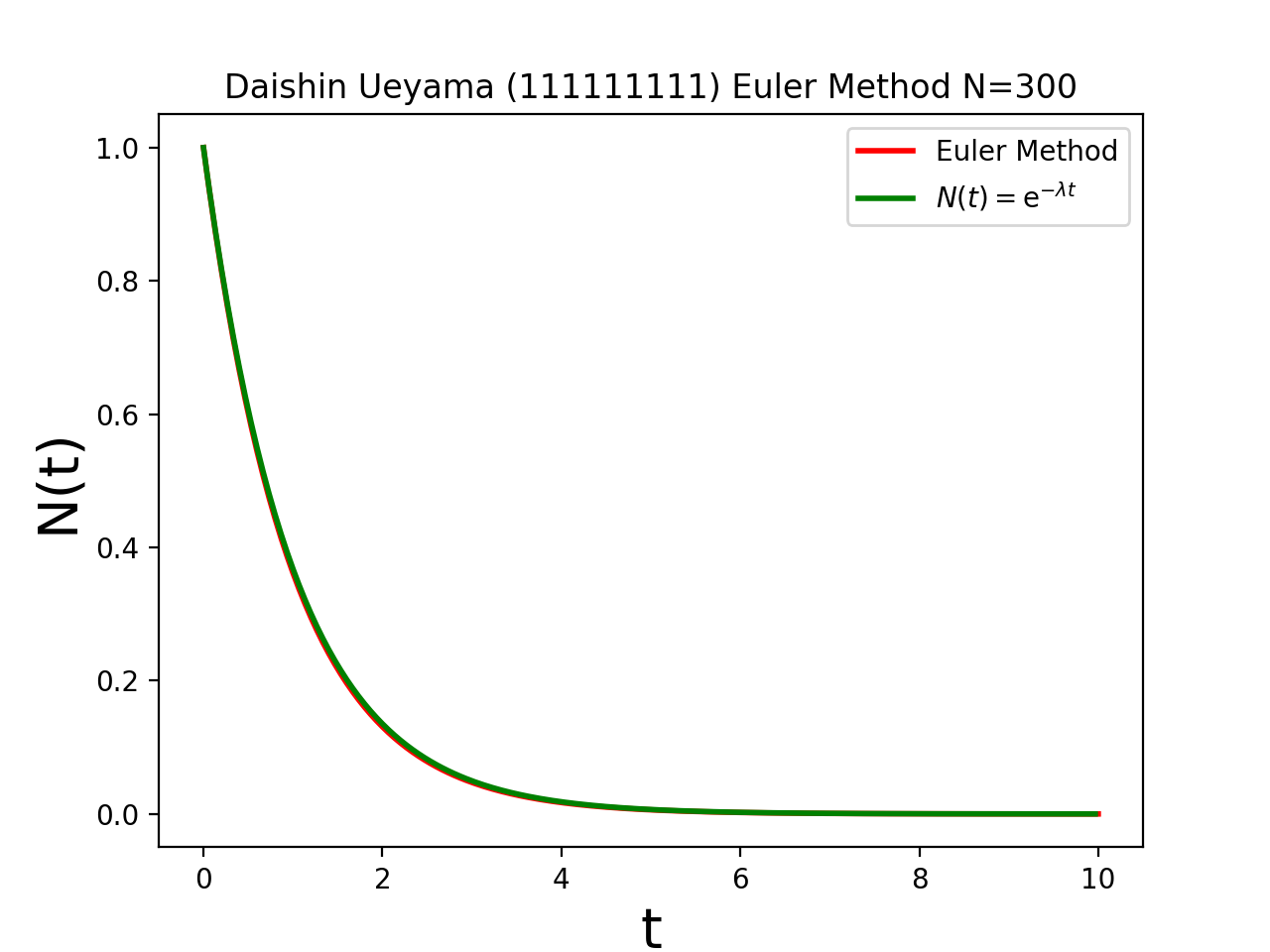
解析的に求めた解(S)とオイラー法で求めた数値解を重ねて描くプログラムを作成せよ.例えば,次のようになる.この例では,解(S)を緑色で描き,数値解を赤色で描いている.(この例では、0≦t≦10 を 100等分している)
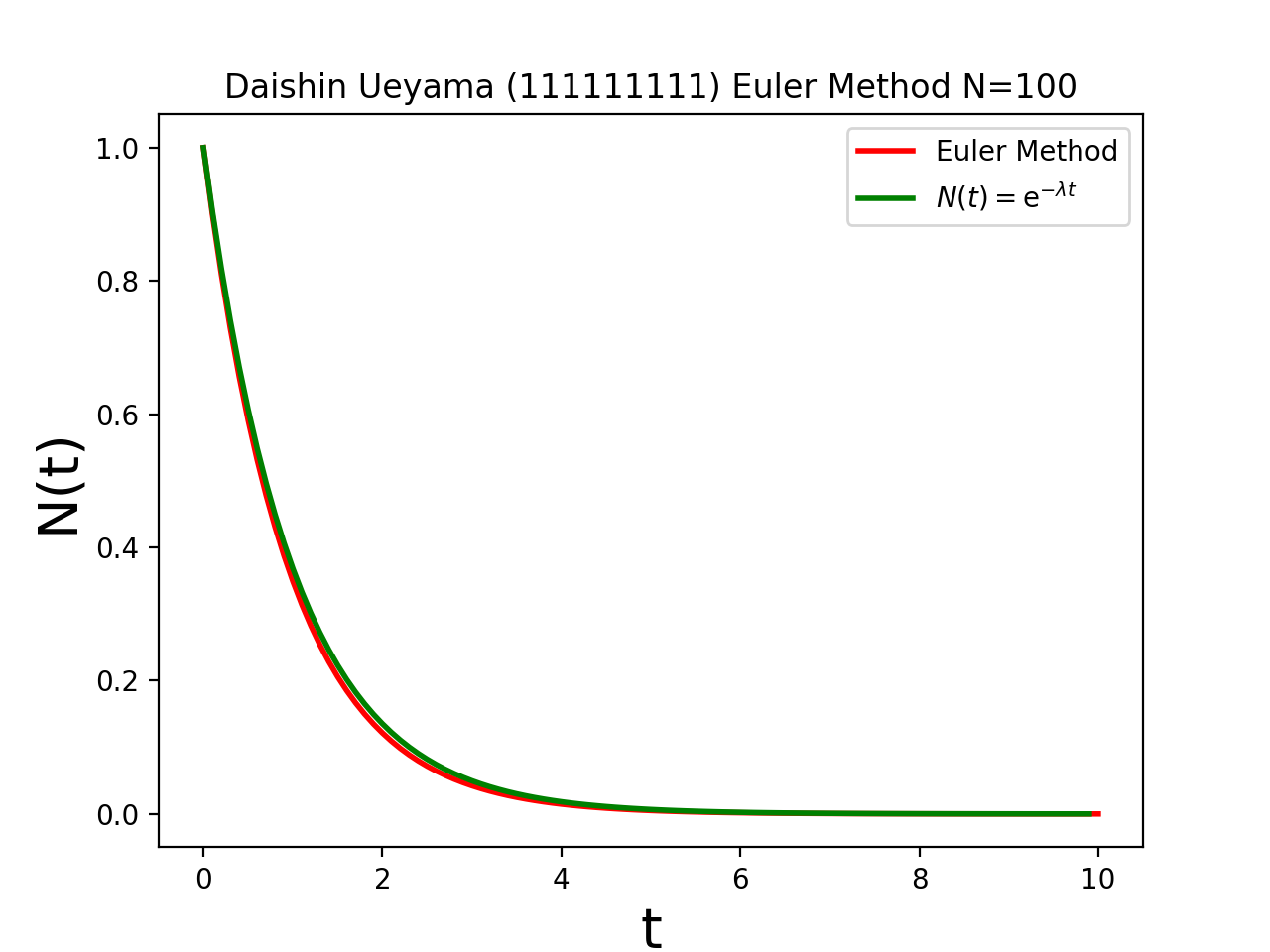
刻み幅を小さくすると両者の差は縮まる.(次の例では、0≦t≦10 を 300等分している)
授業中に作成したファイルを提出してもらいます。