数学を探せ! 「スマートフォン市場のシェアを決めるものはなに?」

写真を見てもなかなか数学は探せませんね。むしろ、新しいスマートフォンが欲しくなったのではないでしょうか? 今やスマートフォンは世界中の人にとって身近な物になっています。ここではスマートフォンの市場シェアは何によって決定されるのか数学を用いて考えてみます。
少し前までは契約している携帯電話会社を変更すると電話番号を変えなければならず、一度携帯電話会社と契約すると乗り換えることは非常に難しかったものです。
しかし、今では私達は手持ちのスマートフォンの電話番号を変更せずに他の携帯電話会社に乗り換えることが出来ます。MNP(Mobile Number Portability)というサービスです。
なぜ各社ともここまで激しく競い合っているのでしょうか?もちろん理由があります。
ここでは市場シェアの問題を考えるために下記の仮定を置きます。
「消費者は次に契約する携帯電話会社を現在契約した携帯電話会社のみに依存して決める(それ以前に契約した会社は考慮しません)」
この仮定はそれほど悪いものではないでしょう。現在、スマートフォンの幾つかのサービスは携帯電話会社独自のサービスとして提供されています。MNPを用い以前より乗り換えやすくなったとはいえ、乗り換えると不便になることも多く一度契約するとなかなか他の携帯電話会社に乗り換えにくい面があります。そのため現在どの会社と契約しているかはとても重要な情報なのです。
また、携帯電話会社としてA社、B社、C社の3つの会社があり消費者の乗り換え行動は下記の表に従うとしましょう。
表1 現在契約している携帯電話会社と次に契約する携帯電話会社の関係
| 現在、契約している携帯電話会社 | ||||
|---|---|---|---|---|
| 現在A社と契約 | B社 | C社 | ||
| 次に契約する携帯電話会社 | 次にA社と契約 | 80% | 20% | 10% |
| B社 | 10% | 70% | 20% | |
| C社 | 10% | 10% | 70% | |
表の見方ですが、表を縦に見ていきます。
1列目は現在A社を選択している人が次に乗り換えずそのままA社を選択する可能性が80%であり、B社に乗り換える可能性は10%、C社に乗り換える可能性は10%であることを表しています。2列目、3列目も同様です。
実は上記の設定に基づき簡単な数式を用いることで「将来のスマートフォン市場のシェアは現在の市場シェアに関わらず各個人の乗り換え行動のみにより決まる」ことを示せます。
数学のどの領域の話か
ここで使う数学は皆さんよくご存じの「連立一次方程式」です。
大学ではこの連立一次方程式の性質も含む学問分野として 線形代数があります。
「線形代数」は行列(ヒトの行列とは違いますよ…)を取り扱う学問で、大学で学ぶ数学の基礎となるものです。微分積分と並んで大学初年度で学ぶ最も重要な学問になります。
また今回の話は確率的に物事が決まっていく行動を取り扱っており、このような分野を確率過程論と言います。
粒子がランダムに動く運動や金融工学も、確率過程の典型例です。(今回の問題では「マルコフ連鎖」と「ペロン・フロベニウスの定理」が検索ワードになります。興味がある人は調べてみてください)
数式を用いた解説
ここでは、個人の選択行動がスマートフォンの市場シェアに与える影響を具体的に調べてみます。
今回はとても単純に考えることにします(この姿勢ははじめの一歩としては間違ってないでしょう)。手を動かして考えることを強くお勧めします。
携帯電話会社としてA社、B社、C社の3つの会社があるので、時刻tにおけるそれぞれの現在の市場シェアを
とします
| A社 | B社 | C社 | |
|---|---|---|---|
| 時刻tにおけるそれぞれの現在の市場シェア |
例えば、時刻tにおいてA社が50%のシェアを占めている場合
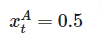
となります。
ここで、現在(時刻 t )契約している携帯電話会社から、次に契約する携帯電話会社を決める確率を表1のように表せることとすると、時刻 t+1 における携帯電話会社Aの市場シェア は、時刻 t における3社の市場シェア を用いて次のように表せます。
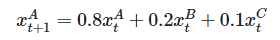
同様に時刻 t+1において事業者B、Cの市場シェア は次のように表せます。
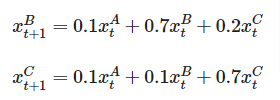
さてここで将来市場シェアはある一定の値に落ち着くとします(「ん!?そんなこと言っていいの?」と思った方は筋が良いです。実はこのことは証明されています)。
将来一定値に落ち着いた3社の市場シェアをそれぞれ と置き上の3つの式に代入します。(一定値に落ち着いていることからA社の市場シェアは となります。B,C社も同様)
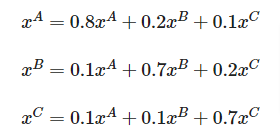
ついに問題は連立一次方程式になりました。未知数3つで3本式があるので解けそうですが、変形すると同じ式が2つ出てきて値を決定することが出来ません。
もう一本条件が必要です。今、市場全体には3社しかありませんから3社の市場シェアの合計は100%になりますので
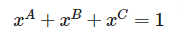
これで条件がそろいました。4つの式を解き3社の市場シェアは次のようになります。
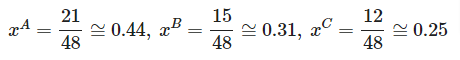
ここで注目してほしいのは上の4つの式に初めのシェアは関わってないことです。
つまり、初期の市場シェアがどんな比率であっても、表1で表された各携帯電話会社間の乗り換え確率だけから将来の市場シェアが決まることが分かります。
現在市場シェアで優位に立っている会社も安心できませんね。
どうでしょう、各携帯電話会社がMNPで自社に乗り換える消費者をあの手この手で増やそうとする理由が分かったのではないでしょうか?
もちろん、今回紹介した例は現実の問題をとても単純化して数式で表しており現実の問題にそのまま使えるわけではありません。それでも、数学を用い限定された条件下で何が起こるのかということをうまく説明できる部分があるということがとても大切です。

担当教員プロフィール
1973年千葉県生まれ。コンピュータ好きです。
准教授 木下 修一
高校までは計算することが得意で、他の科目に比べて覚えることが少ないことが数学を好きになった理由です。特に方程式はお気に入りで生物現象や社会現象も方程式で扱えないかなぁ…とよく夢想したりして過ごしていました。担任の先生に相談したところ、それならば物理学科に進みなさいとアドバイスを受け進学し、現在は発生や進化といった生物現象を数学、物理、コンピュータを用いて研究しています。数学は研究のための道具ですね。今後は高校生の頃の夢も思い出し生物現象だけじゃなく社会現象なども研究していきたいと計画中です。
3分でわかる数理工学講座バックナンバー
第1回「スマートフォン市場のシェアを決めるものはなに?」
第2回「雨粒とDNA」
第3回「蛇口から出る水」
第4回「パターンに潜む数理」
第5回「個体間にみられるコミュニケーションと数理工学」
第6回「エネルギーで楽をする話」
第7回「対称性と周期性」
第8回「競争している生物の個体数を予測しよう」
第9回「血管新生」

