数学を探せ！ 「対称性と周期性」
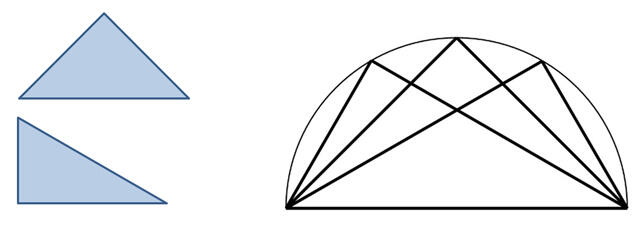
三角定規を使っていますか？三角定規の形は、直角２等辺三角形と、正三角形の半分です。この２つの三角形はプラトンの要素三角形（ストイケイア）と呼ばれます。
この２つの三角形から正三角形と正方形を作り、それから４つの正多面体、正４面体、立方体、
正８面体、正２０面体を作ることができます。プラトンは大胆にも、それらを「火」、「土」、「空気」、「水」に対応させ、５つめの正１２面体には「宇宙」を対応させたと言われています。
正多面体は３次元空間にある非常に対称性の高い図形ですが、平面上にはたくさんの種類の正多角形（正三角形、正方形、正５角形、正６角形、正７角形、正８角形…）があります。
次に平面の周期的な模様を見てみましょう。卜部東介氏のウェブページhttp://tsuboiweb.matrix.jp/urabe/public_html/urabe/「文様の幾何学」には、日本の着物の柄には以下の１７種類があることが記されています。
平面の周期的な模様は２つの方向の方向の平行移動で重なります。
この１７種類を眺めていると、特にリストの下半分の模様には、９０度、１２０度、６０度という角度が良く出てきます。周期性と対称性をもつ図形には三角定規の形（ストイケイア、要素図形）が隠れています。
これはどの領域の話か
この周期性のある対称な模様から見えてくる数学は何でしょうか？
周期性も対称性も平面の図形を移動して重ねることができるかどうかという問題です。ひとつの移動は、回転と平行移動で記述されます。ひとつの移動で重ねることができ、つぎに別の移動で重ねることができるとき、それを続けて行った移動で重ねることができることになります。これらの移動の全体は、「群」と呼ばれる構造を持っているものになります。その群が17種類だということですし、その中に現れる回転に出てくる角度は、９０度、１２０度、６０度にならなければいけないということがわかります。
数式を用いた解説
平面の移動を定義することから始まります。
【定義】平面
の「移動」とは、写像
で2つの点の間の距離（2点を結ぶ線分の長さ）を変えない
もののことである。
ここで、
はベクトルの大きさ、すなわち、
に対し、
である。
平面の移動は、ベクトルと行列を用いて書かれます。
【命題】 平面の移動は、
または
として、
の形に書かれる。
平面の移動全体は、次の性質をもちます。
平面の2つの「移動」
を続けておこなったもの
は「移動」である。
3つの移動
に対し、
「移動」
した後、逆向きの「移動」
をおこなうと「移動しない移動」
（恒等写像）になる
この性質を持つことを群をなすといいます。
図形の対称性は、図形
を自分自身に映す「移動」が、どれくらいあるかで決まります。
図形を自分自身に映す「移動」の全体をの等長変換群と呼び、
と書きます。
合同変換群と呼ぶこともあります。
周期的に繰り返す図形は周期だけの平行移動が図形を自分自身に映します。
格子模様は、2つの方向の平行移動で模様が重なります。すなわち、周期的な図形（模様）とは、等長変換群が格子を含むような図形です。
格子とは、2つの平行ではないベクトル
の整数倍の和で表される集合です。
格子の形状にもいろいろなものがあり、平坦トーラスのモジュラスにより分類されます。
より直観的に説明すると、格子に対して次のようなディリクレ領域あるいはボロノイ領域と呼ばれる図形
が定まります。
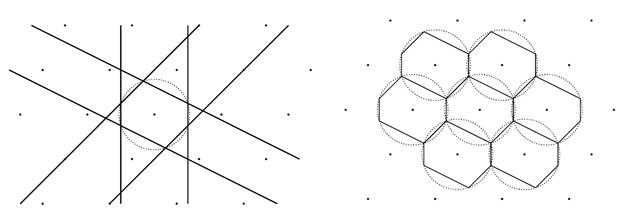
図形は円に内接する、対辺が平行で長さが等しい6角形で、2つの頂点が近づいて合わさったとき4角形（長方形）となります。
このことから、格子が回転で自分自身に移るとき、この図形は、長方形、円に内接する線対称な６角形、正方形、正６角形でなければならないことがわかります。
格子が回転対称性を持つとき、それは180度回転、90度回転、120度回転、60度回転のいずれかです。
このことが、周期性と対称性をもつ図形に三角定規の形（ストイケイア、要素図形）が登場する理由です。
参考：http://ocw.u-tokyo.ac.jp/course_11377/
担当教員プロフィール
特任教授 坪井 俊
1953年広島生まれ。中学で出会ったユークリッド幾何に感じた面白さが大学での研究の原点になったのかもしれません。これまで曲面を一般化して考えられる多様体という空間の対称性を記述する微分同相群を中心に研究してきました。2019年から本大学の授業の中では、「折り紙と数学」や「平面幾何と数学のあゆみ」というテーマを取り上げています。
※この講座の著作権は著者にあります。無断引用や転載等はお断りいたします。
３分でわかる数理工学講座バックナンバー
第１回「スマートフォン市場のシェアを決めるものはなに？」
第２回「雨粒とDNA」
第３回「蛇口から出る水」
第４回「パターンに潜む数理」
第５回「個体間にみられるコミュニケーションと数理工学」
第６回「エネルギーで楽をする話」
第７回「対称性と周期性」
第８回「競争している生物の個体数を予測しよう」
第９回「血管新生」
