数理工学科

数学を探せ！「パターンに潜む数理」

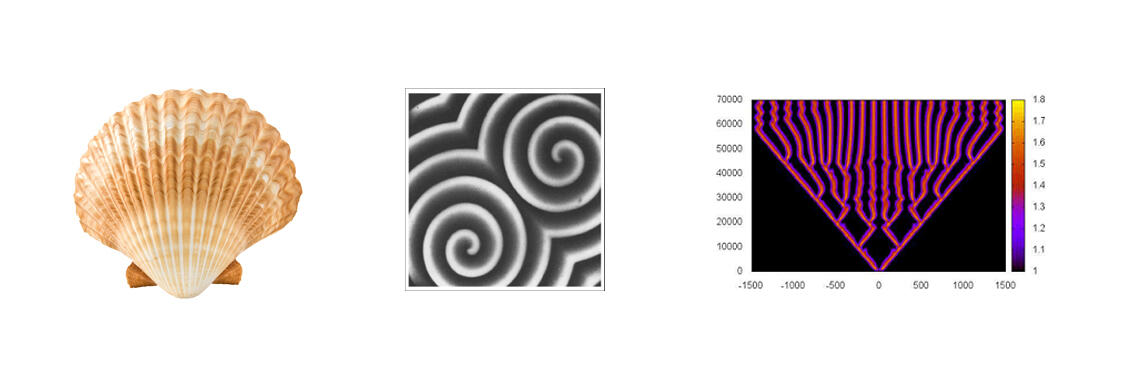
砂浜を歩いていると打ち上げられた貝殻が見つかることがあります。その貝殻を手に取ってみると表面にさまざまなパターン（模様）を見ることが出来るでしょう。１番の写真は、貝殻とそのパターンの一例です。さて、貝殻に限らず多くの生き物の体の表面には様々なパターンがあります。貝殻以外で代表的なものを挙げると、キリンの斑模様やシマウマの縞模様などです。こういったパターンはどの様に形成されるのでしょうか？一つの説明として、「体の表面にある化学物質の濃度の場所ごとの違いによって形成される」というものがあります。パターンが形成される過程で、化学物質は生き物の体の表面上で自発的に拡がっていきます。この現象を拡散現象と呼びます。また、化学物質は１種類とは限らず複数種あることがあり、お互いに反応を起こし、別のものに変化したりします。化学物質の拡散現象と化学物質同士の反応によって様々なパターンが観察される実験の一つにBelousov- Zhabotinsky反応（BZ反応）というものがあり、そのパターンの一例が２番の写真［１］です。

ところで、この拡散現象と化学反応による説明に基づいてパターンが形成される様子を再現するにはどのようにすればよいのでしょうか？一つの方法として、微分方程式を使って現象を定式化（数理モデル化）し、計算機で計算するという手法が挙げられます。今回は、反応拡散系と呼ばれる連立の微分方程式を用いて、化学物質の濃度の各時刻における場所ごとの変化を記述し、化学物質の濃度が場所ごとにどのようになっているかを計算機に計算させます。ここでは、反応拡散系の一つとして知られているGray-Scottモデルを紹介します。

数学のどの領域の話か

今回挙げた反応拡散系は、偏微分方程式の一つでもあります。偏微分方程式とは、微分方程式の一種で、「微分を含む、“ある条件”を満たす“多変数関数（すなわち２つ以上の変数の関数）”は何でしょうか？」と問う問題なのです。そして、微分方程式の解を調べるためには、解析学すなわち微分・積分といった分野の手法を使うことになります。また、微分方程式を導出する際には、化学の反応速度論の考え方も用いています。

さらに、計算機に微分方程式を計算させるために数値解析という分野の知識も必要となります。計算機は、微分方程式を直接計算することが出来ません。そこで、計算機が計算できるように、微分方程式を離散化する必要があります。この離散化という操作で差分方程式が得られるのですが、この差分方程式は、高校数学の数列の単元で学習する漸化式の複雑なものとなっています。つまり、漸化式を計算することでパターンが形成される様子を観察できるのです。

数式を用いた解説

写真に使われている数式

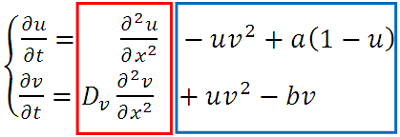
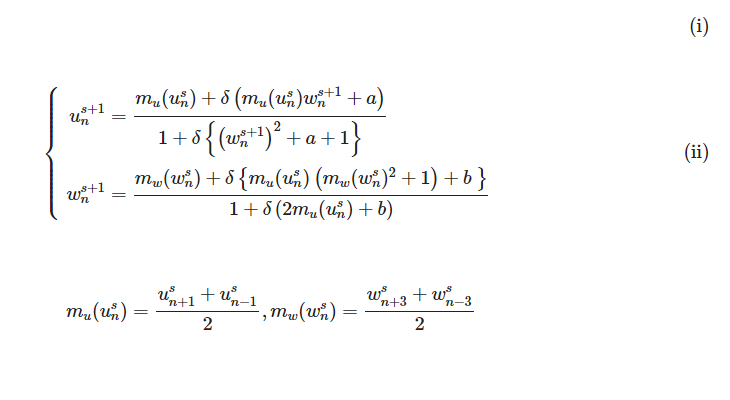
解説

(ⅰ)が反応拡散系の一つで、ある化学反応を数理モデル化したGray-Scottモデルと呼ばれる連立の偏微分方程式です。 $u, v$ はそれぞれ二種類の化学物質のある時刻におけるある場所の濃度を表しており、時間の変数 $t$ 、空間の変数 $x<script type="math/tex" id="MathJax-Element-6">x$ の関数で $u(t, x), v(t, x)$ を表しています。また、 $\frac {\partial u} {\partial t}$ や $\frac {\partial^2 u} {\partial x^2}$ はそれぞれ多変数の関数に対して $t$ に関する一階 $x$ に関する二階の微分で偏微分と言います。この二つの方程式は二種類の化学物質の濃度の時間変化がどの様になっているかを表しています。赤い四角に囲まれた部分は、物質の拡散現象を表す項で拡散項と呼びます。一方、青い四角で囲まれた部分は二種類の物質の化学反応による効果を表す項で反応項と呼びます。そして、 $a, b, D_v$ はパラメータです。このパラメータを変えることで様々なパターンが得られます。

(ⅱ)は(ⅰ)のGray-Scottモデルを離散化して得られた漸化式で、 $\delta$ は正のパラメータです。高校までだと、漸化式で求める数列の一般項 $a_n$ の添え字は、 $n$ の一つだけですが、今回の場合はといったように添え字が $s, n$ の二つとなっており、複雑になっています。この漸化式を計算機に計算させた結果の一例が、3番の写真です。縦軸が時間に関する変数 $s$ 、横軸が空間に関する変数 $n$ に対応し、 $w$ の値を色で表した図となっています。

今回は、パターンが形成される様子を数理モデル化した偏微分方程式を計算機で計算し、現象がどうなっているかを観察することが出来ました。パターン形成に限らず、様々な現象を微分方程式で数理モデル化し、計算機で計算し現象の解明につなげることが出来ます。あなたはどんな現象を調べてみたいですか？

参考文献

[１] S. C. Muller, T. Plesser, and B. Hess. “Two-dimensional spectrophotometry and pseudo-color representation of chemical patterns.” Naturwiss., 73(1986), 165-179.

担当教員プロフィール

准教授　松家　敬介

高校までは、複雑な計算を経て方程式を解くといった数学自体の内容に対して魅力を感じていました。しかし、大学で数学をはじめとして物理、化学さらに生物と混在した学際領域の学科に進み、数学とさまざまな分野が融合した領域にも興味をもつようになりました。数学を新しい場面で如何に応用できるかを考えていくことで数学に対する魅力をより一層感じる様になりました。

今回紹介した話題は、「生物」に出てくるパターンを拡散現象という「物理」の現象と化学反応という「化学」の内容で説明し、そして、それらを「数学」で記述するといったようにさまざまな分野にまたがったものとなっています。数学はもちろんのこと、さまざまな分野についても積極的に吸収していくことで、視野が広がり、自分が本当に面白いと思える新しいものに出会えるのではないでしょうか。

３分でわかる数理工学講座バックナンバー

第１回「スマートフォン市場のシェアを決めるものはなに？」
第２回「雨粒とDNA」
第３回「蛇口から出る水」
第４回「パターンに潜む数理」
第５回「個体間にみられるコミュニケーションと数理工学」
第６回「エネルギーで楽をする話」
第７回「対称性と周期性」
第８回「競争している生物の個体数を予測しよう」
第９回「血管新生」

数学を探せ！ 「パターンに潜む数理」