数理工学科

数学を探せ！「蛇口から出る水」

水道の蛇口を弱くひねると水はきれいにまっすぐ落ちます。このとき、写真のように、水流は下にいくほど細くなります。子どもの頃から見慣れていますよね。
なぜ下のほうが細くなるか、分かりますか？
そうです。重力によって水の落下速度がだんだん速くなるからだろうと、想像がつきますね。
では、このきれいな水流の形は数学的にどのような関数で表されるでしょうか？

数学のどの領域の話か

これは物理学における力学の問題で、地上における自由落下運動に関係しますが、単独の物体の落下ではなく、水という流体の連続的な運動に関するものです（連続体の力学）。今回は高校の物理と数学の知識だけで解ける式を扱いますが、一般的には空間と時間に関する微分方程式を解くことが必要になります。

このような問題は工学でも重要です。というのは、工業生産において流体を扱うことはごく一般的だからです。たとえば、石油精製、化学合成、医薬品、食品製造など、素材としての液体を扱う場合だけでなく、プラスチックや金属なども高温で溶かして成型しますし、さまざまな製品の加工や洗浄にも水を多用します。こうした工場では装置や配管の中の流体の流れを正確に把握し、制御する必要があり、そこでは数理工学を使った設計が欠かせません。

数式を用いた解説

写真に使われている数式

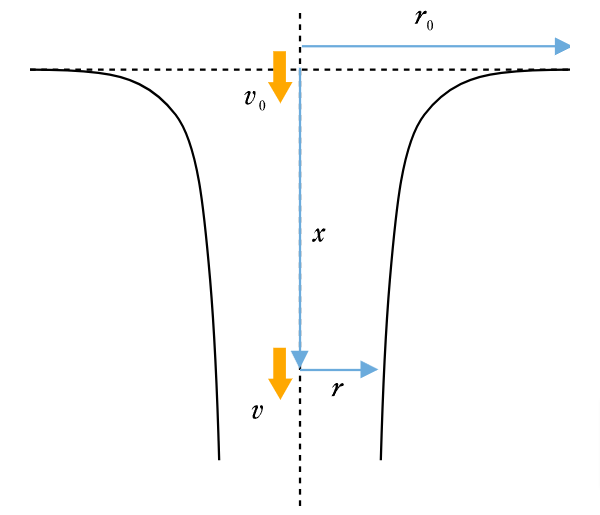
水道の蛇口から出る水流は鉛直軸の回りに軸対象、つまり水流の水平断面は円であるとします。蛇口から下方向に距離 $x\mathrm{(cm)}$ の位置における水流の半径を $r\mathrm{(cm)}$ とします。
蛇口の出口の内径を $r_0\mathrm{(cm)}$ 、そこでの流速を $v_0\mathrm{(cm/s)}$ とし、重力の効果だけを考えた単純なモデルを解くと、半径 $r$ は $x$ の関数として次のように表すことができます。

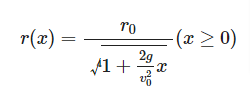
ただし、 $g$ は重力加速度（ $\cong 9.8 \mathrm{m/s^2}$ ）です。
この関数形を最初の写真に重ねてみると、だいたいうまく水流の形状と一致することが分かります。

解説

蛇口から出る水にはたらく重力を考えます。
水流の中の小さな部分（質量 $m$ とします）を想像してください。それが重力を受けて次第に下向きに加速され、 $x$ だけ落下したときの速度を $v$ とすると、エネルギー保存則により、運動エネルギーの増加は位置エネルギーの減少と一致しますから、

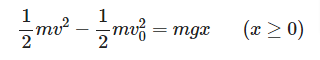
が成り立ちます。すなわち

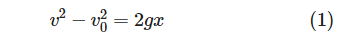
となります。
一方、水の流量は断面積 $πr^2$ に速度 $v$ を掛けたものですが、これがどの位置でも一定であることから、

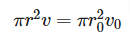
が成立します。すなわち

です。式（１）と式（２）から $v$ を消去すれば $x$ と $r$ の関係が次のように求まります。

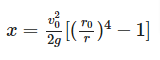
ここで $x \geq 0$ は $r \leq r_0$ に対応します。この式から逆に $r$ を $x$ の関数として表せば

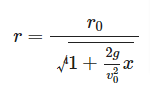
となります。
なお、 $x$ と $r$ はともに長さの次元をもっていますが、特徴的長さ $x_{c}\equiv \frac{v_{0}^{2}}{2g}$ というものを定義し、無次元の変数 $X\equiv \frac{x}{x_c}$ 、および $R\equiv \frac{r}{r_0}$ を導入すると、上の式は

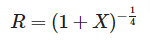
という一つの簡潔な式で表現されます。
これが意味するところは、水流の形は水平方向、垂直方向をそれぞれある倍率で拡大ないし縮小させれば、一つの関数に帰着するということです。物理的には異なる状況が数学的には本質的には同一であるということは、数理の面白さのひとつです。

モデルの適用範囲

得られた関数を、流速 $v_0=5,10,20 \mathrm{cm/s}$ の３つの場合について、 $x$ が 0～3 $\mathrm{cm}$ の範囲で描いてみたものが次のグラフです。（ $x$ 軸が縦方向になるよう90度回転させて表示しています。）

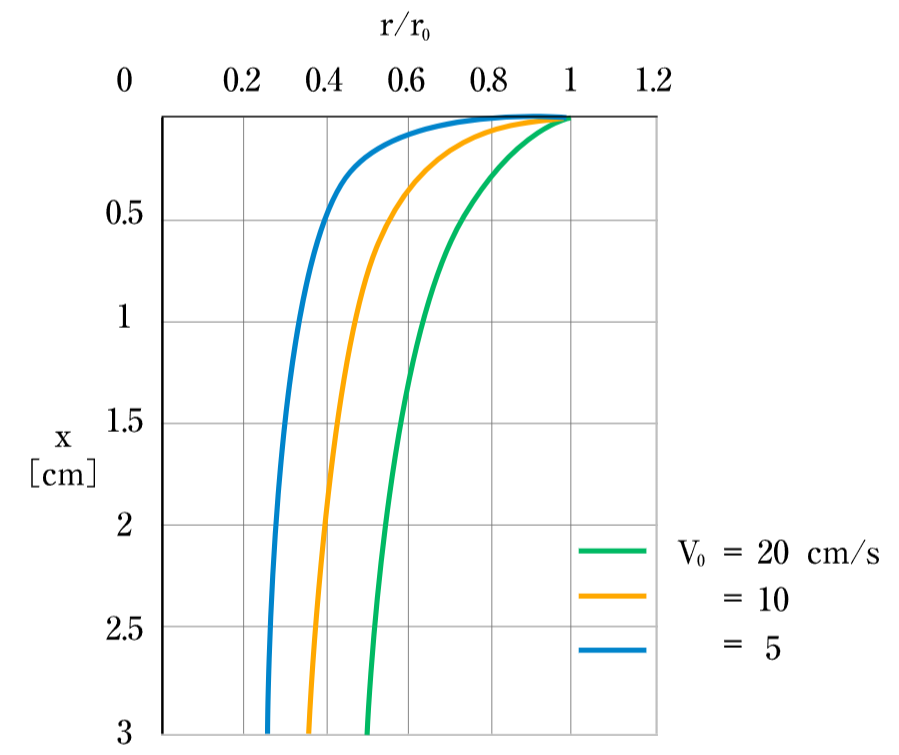
これは実際の水流の形状と比較的よく合っていますし、流速 $v_0$ によって水流の太さが変わる様子も再現されています。
ただし、水流の形状の細かいところまで正確に一致するとは限りません。
上の写真との比較でも、蛇口の出口付近ではややずれがあるようにも見えます。
実際、蛇口付近の微小な領域では、表面張力や金属管との相互作用（濡れ）など、重力以外の要因も絡んできます。水流が水平面内で一様であるという仮定も正しいとは限らず、水流の中心付近と表面付近で流速が異なる可能性もあります。こうしたことは蛇口の構造や材質にもよるかもしれませんから、実験も条件を注意深く設定する必要が出てきます。
このように、簡単な数式が現象の本質を捉えている場合でも、より正確に記述するためには、より精密な実験と、より詳細なモデルを用いた解析が必要になってきます。

さらに、このモデルにはより本質的な意味での適用限界があります。
式の上では $v_0$ を小さくすると半径 $r$ はいくらでも小さくなりますが、実際にはご存じのとおり、蛇口を絞って水があまりに細くなると、表面張力によって途中から水滴になって落ちるようになります。
逆に $v_0$ をどんどん大きくすると、式の上では、ほとんど真っすぐな円柱に近づくはずですが、実際は蛇口を大きく開くと、水は水圧によって勢いよく飛び出し、乱れた水流になることも経験で知っています。
こうした状況を扱うにはより高度な数理モデルが必要になります。

担当教員プロフィール

教授　阿部　修治

私が数学を好きになったきっかけはよく覚えていませんが、中学校の頃からいろいろな関数のグラフを描いてみることは好きでした。数式そのものは無味乾燥なものですが、グラフという目に見える形にすると、現実世界とのつながりが出てきて、いろいろ想像をかきたてるのです。その後、物理学を学び、現実の材料の性質を数理を用いて研究するようになったのは、そうした興味からかもしれません。コンピュータがグラフを描いてくれるようになった今でも、手書きでグラフをおおざっぱに描いて楽しむ習性は変わりません。

３分でわかる数理工学講座バックナンバー

第１回「スマートフォン市場のシェアを決めるものはなに？」
第２回「雨粒とDNA」
第３回「蛇口から出る水」
第４回「パターンに潜む数理」
第５回「個体間にみられるコミュニケーションと数理工学」
第６回「エネルギーで楽をする話」
第７回「対称性と周期性」
第８回「競争している生物の個体数を予測しよう」
第９回「血管新生」

数学を探せ！ 「蛇口から出る水」