数学を探せ！ 「個体間にみられるコミュニケーションと数理工学」

携帯情報端末（スマホ）やソーシャルネットワーク（SNS）というコミュニケーションツールが莫大な富を生み出す現代社会を見ると、各個人が他者とのコミュニケーションを真に欲していることがよくわかります。一方で、人間以外の生物でも、他者とのコミュニケーションを頻繁に行っている例がよく見られます。例えば社会性昆虫として有名な蟻はお互いの触覚を触れ合わせることで頻繁に「会話」をし、なんらかの情報交換をしているという観察事実が多数報告されていますが、その目的となると諸説あるもはっきりしません。

私は、生物に見られる個体同士のコミュニケーションの1つの大きな目的が、役割分担の決定ではないかと考えています。人間を含め、多くの生物は次の世代に生命をつなげるために、巧妙に役割分担を行います。先の蟻の例でも、コロニー内で採餌や子育てといった役割分担が適切に行われますが、ただ分担すれば良いわけではなく、役割分担の「個体数比率」（全体におけるバランス）が適切に実現されなくてはなりません。つまり、全員が餌を採りに行きたいと希望しても困るわけです。会社のような組織であれば、リーダーが全体の仕事量などから役割分担を指示しますが、蟻など多くの生物で、そのようなリーダーはいないという状況証拠があるにもかかわらず、適切な役割分担がなされ、大きな謎となっています。

数理的な考え方の解説

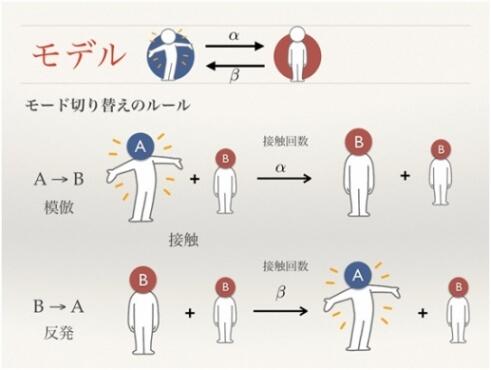
図1：二つの状態（モード・役割）A、Bの遷移を示した概念図。Aという状態にある個がBという状態にある他者と出会うと、出会った回数がαを越えるとBという状態に変化する。一方、Bという状態の個が同じくBという状態の他者と出会う回数がβを越えるとAという状態に変化する。これを繰り返す。

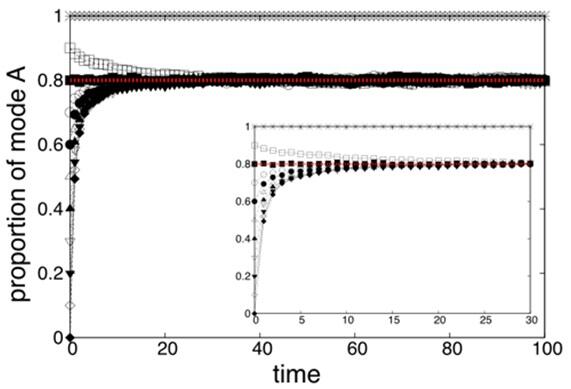
図2：図1を表現した数理モデルのシミュレーション結果。様々な初期比率からスタートしても、時間とともに一定の比率に近づく様子がわかる。

そこで数理モデル（図1）を用いてシミュレーションを行うと、個体間の接触と情報交換を繰り返すと、効率よく役割分担の個体数比率を調整できることが分かりました（図2）。この結果は、社会的枠組みとしての役割分担が、個体間の局所的なコミュニケーションのみ、すなわちリーダーを置くことなく決定できることを示しています。ここでは、A, Bという二つの役割のみを考えましたが、複数の役割への拡張ももちろん可能です。また、これはメタモデル（概念モデル）とでもいうものですが、このメカニズムの結論として比率が決まることは、個体数がとても多く密度もとても高いといった仮定を置くことで数式化され、数学として現象を理解できます。但し、その仮定が現実を逸脱していないかどうかは絶えず気にかける必要があります。数理工学の立場として、メタモデルを経由した現象の理解と応用が一つの道筋と言えるでしょう。

ところで、このような仕組みが、本当に生物で用いられているかは検証が必要となりますが、機構の利点を活かした工学的な応用は幾つか考えられます。例えば災害時のように通常のインフラが使えない状況で役立つのではないかと考えています。大きな災害が起こると、それまで普通に使えていた携帯電話等が利用できない状況が生まれ、個々が孤立することになります。しかしながら、複数の避難所へそれぞれの避難所の収容人数を考慮した避難誘導等が必要となるでしょう。紹介した仕組みは、携帯ネットワークが破壊され、全体を見て個々を誘導することが難しい状況においても、個人の携帯端末が発する近距離通信波（Bluetooth等）を用いた、近距離の通信さえ行う事ができれば機能するため、適切な複数避難所への振り分けが可能となるでしょう。

また、近未来では自律制御で運動する様々な移動体が数多く存在する世界になりそうです。例えば、自動運転カーや配達ドローンなど、しかもそれらが数多く身の回りを動き回り、集団として秩序をもって運動する必要があります。それらは、まるで鳥の集団や動物の群れのように見える事でしょう。そのような自立制御によって運動する移動体の制御についても、紹介した仕組みは有効であると考えています。集中的な管理は可能かもしれませんが、例えばそれらが使えなくなるような非常時においても安全に運動を続けるには、局所的なコミュニケーションのみからなる制御のメカニズムを持つ必要があります。そのような制御方法の一例となり得るのではないかと考えています。

数学って何の役に立つの？

中学・高校の数学で身につく論理的思考力は、大学数学でさらに強化され、社会の様々な問題を論理的に捉え、解決する為の大きな力となります。具体的な問題（例えばここで紹介した「全体におけるバランスの問題」）では、その個々の問題の特徴に強く捕らわれてしまいますが、数学が持つ抽象性は、そのような具体性から良い意味で距離を置くことができ、思考の飛躍（イノベーション）をもたらします。実際、ここで紹介したお話は、「全体におけるバランス問題」とは関係の無い他の数学的な問題の検討から得られたアイデアが出発点となりました。数学って何の役に立つの？とよく話題になりますが、数学的な考え方はどのような職種に就くにしても必ず役立つと私は思っています。

担当教員プロフィール

教授　上山 大信

1970年山口県生まれ。
お寺の生まれで、小さい頃から人に接することが多い環境で育ちました。異なる個性を持つ人々の間で思想という目に見えず、簡単には捉えられないものが時代を超えて伝わり、社会を形成する一つの要因となっていることは、数理とは一見かけ離れた問題ですが、今回の研究を通じて少し糸口が見えてきたように思います。コミュニケーションの役割という興味から得られた数理的な見地は、工学的な問題と組み合わさることで、身の回りをより安全で便利にするアイデアがうまれることがあります。生物や化学の世界に見られる不思議な現象を数理的な見地で理解し、それらを応用することは数理工学の一つの立場でしょう。一見関係が無いと思われる事が、数理を通して繋がることはとてもエキサイティングな事です。今後も、自分が得意とする視点から、数理を活用した新たな研究分野を開拓していきたいと思います。

３分でわかる数理工学講座バックナンバー

第１回「スマートフォン市場のシェアを決めるものはなに？」
第２回「雨粒とDNA」
第３回「蛇口から出る水」
第４回「パターンに潜む数理」
第５回「個体間にみられるコミュニケーションと数理工学」
第６回「エネルギーで楽をする話」
​第７回「対称性と周期性」
​第８回「競争している生物の個体数を予測しよう」
第９回「血管新生」