数理工学科

数学を探せ！「雨粒とDNA」

雨粒の落下

今回は、数理の目で見ると、世の中意外なものどうしが似通っているというお話です。
最近日本の亜熱帯化が進んでいるのかゲリラ豪雨がよく起こります。ゲリラ豪雨に打たれると痛いほどです。ところで、激しい雨のときと霧雨のときは雨粒の落下速度は同じでしょうか？
霧雨のときは、雨粒は何となくゆっくり落下しているように感じますが、ゲリラ豪雨の雨粒は大きいだけでなく、より激しく打ちつけているように感じます。実際どうなのでしょうか。
この問題は、「もの」のサイズによって落下速度が変化するかどうかという問題です。実は、これは生化学の分野で、DNAをそのサイズで分離しようとするときの問題と似通っています。

ヒトゲノム計画

約10年前に完了して、iPS細胞などその後の生命科学の大躍進のもととなった「ヒトゲノム計画」を推進するためには、多くの革新的な技術の開発が必要でした。その中の一つにDNAの地図作り（マッピング）というものがあります。
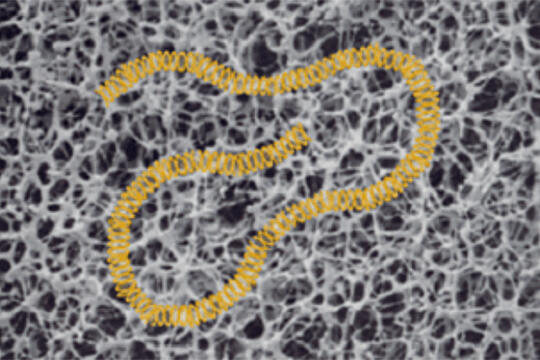
ヒトのDNAは長大です。一つの細胞の中に全長２mに達するDNAが格納されています。いきなり細かい部分の配列情報を読み取ることはできず、目印となる部分がどのように配置されているかを調べることから始まります。そのために、切断された複数のDNA断片の長さを調べる技術が必要でした。ゲル電気泳動がその技術です。
これは、寒天状の網目でできた分子の中を電圧をかけてDNAを移動させ、DNAの長さによって移動速度が違うことを利用して、長さの異なるDNAを分離するものです（図１）。

落下運動の終端速度

ここで、やっと最初にお話しした雨粒の落下速度の問題と重なってきました。
後で具体的に導きますが、雨粒が球状だとして空気との間の摩擦力が球の表面積に比例すると仮定しますと、落下開始後十分時間が経った後では雨粒は雨粒の半径に比例した一定の速さで落下すると考えられます（終端速度）。これは雨粒でなくても球状の均一な物質であれば成り立ち、また実際には半径の大きさによって半径への依存性は異なりますが、少なくとも半径r の増加関数となります（図２（a））。
それでは球状でない場合はどうなるのでしょうか。例えば太さが一定の棒状の物質の場合は、重力と摩擦力がどちらも棒の長さに比例すると考えられますので、重力と摩擦力の比で求められる落下速度は棒の長さには依存しないことが導かれます。
このように、物体の落下速度は、摩擦力を考えると物体の形状に大きな影響を受けることがわかります。

DNAゲル電気泳動

実は、これと似たようなことがDNAのゲル電気泳動の場合にも生じていたのです。
長大なDNA（約10万塩基の長さ）をゲル電気泳動すると、DNAは電圧を掛けられた方向に伸びて棒状になることが知られています（図２（b））。DNAにかかる電気力はDNAの各部分が電荷を持っていますので、DNAの長さに比例します。またDNAが受ける摩擦力は、DNAが棒状になっていますとDNAの長さに比例します。よってDNAの移動速度は電気力と摩擦力の比で求められますので、DNAの長さに依らないことになります。すなわち長さによって分離できないのです。この状況は、棒状のものの落下の場合とそっくりです。

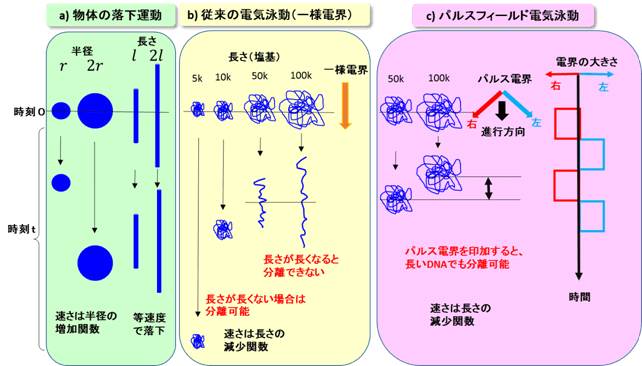
DNAがあまり長くない場合は、DNAは棒状にならず丸まっています（図２（b））。ここでは詳しい理屈は述べませんが、この場合は摩擦力がDNAの長さの２乗に比例するようになり、その結果、電気力／摩擦力であるDNAの速さはDNAの長さに反比例するため、長さによる分離ができるようになります。
しかし、DNAが長くなると棒状になり、棒の落下と同じ理屈で分離できなくなり、マッピング作業がなかなか進まないという問題がありました。

パルスフィールドゲル電気泳動

ここからは、この問題を解決する技術のお話です。
以上お話しましたように、ものやDNAが分離できないのは、落下の場合も電気泳動の場合も、対象が棒状になってしまい摩擦が棒の長さに比例することが本質的な原因です。つまり分離をさせるには、棒状でなくしてしまえばいいのです。そのような技術として、パルスフィールド電気泳動というものが開発されました。
これは、図２（c）に示すように電圧をかける方向を一定の時間間隔で互いに直交する二つの方向に周期的に変更し続けることにより、長大なDNAでも長さによる分離を可能にする技術です。一定の時間間隔を、DNAが電圧の方向に伸びるのに要する時間付近に設定することで、DNAは一定方向に伸びきることがなく丸まった状態を保てるため、長さによる分離が可能になると考えられています。
こわれかけた電気製品は揺すってあげることでたまに復活したりしますが、ひも状のDNA分子の分離に揺することが有効とは面白いなあとこのニュースを聞いたときに感じたことを思い出します。パルスフィールド電気泳動は約30年前に開発された技術ですが、ヒトゲノム計画の進展に大いに寄与し、また今でも細菌のDNAの検出などに活用されています。

まとめ

物の落下の場合、球状であれば十分時間が経った後の落下速度は半径の増加に伴って増大するが、棒状の場合は棒の長さに依存しない。
DNAのゲル電気泳動の場合、DNAの長さが長くないとDNAは丸まっており泳動速度はDNAの長さに反比例するが、DNAの長さが長くなるとDNAは棒状になり泳動速度はDNAの長さに依存しなくなる。
二つの場合で、棒状の「もの」の移動速度は「もの」の長さに依存しないことがわかるが、DNAの場合には、パルスフィールド電気泳動という技術が長いDNAでも棒状にならないようにすることによって長さによる分離を実現し、ヒトゲノム計画に貢献した。

数学のどの領域の話か

雨粒の落下の話は、高校のレベルの力学の話です。DNAの電気泳動の話は、分析化学という分野です。数学的にはブラウン運動の話で、その応用であるレプテーションモデル（蛇行モデル、DNAが蛇のように動いていくというモデル）というモデルが用いられています。

数式を用いた解説

⑴ 雨粒あるいは一様な材質でできた球状の物質の落下運動について考察する（図２（a））。

雨粒または物体は重力によって下方に加速度運動を行う。その後、速度の増加に伴って加速度 $a$ が $v$ になるまで摩擦力が増大し、一定速度（終端速度） $v$ になる。簡単のために摩擦力の増大が速度 $v$ に比例するとすれば、 $\mu$ を摩擦係数、 $m$ を物質の質量、 $g$ を重力加速度として、 $ma=mg-\mu v=0$ が成り立つ。

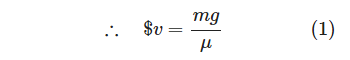
物体が半径 $r$ の球状の場合、

球の質量 $m$ は球の体積 $V$ に比例する。摩擦係数 $\mu$ の半径 $r$ に対する依存性は、半径 $r$ の大きさによって異なることがわかっているが、ここでは簡単のために球の表面積 $S$ 、すなわち $r^{2}$ に比例するとすれば、

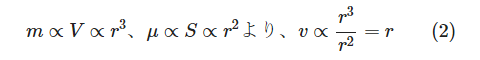
ここで、 $\propto$ は比例記号である。
すなわち落下速度は、球の半径 $r$ に比例する。
実際は半径 $r$ の大きさによって摩擦力の半径 $r$ 依存性が変化するので、この依存性は変化するが、少なくとも半径 $r$ の増加関数となる。

物体が半径 $r$ で長さが $l$ の棒状の場合、

球の質量 $m$ は棒の体積 $V$ に比例し、摩擦係数 $\mu$ は棒の表面積 $S$ に比例すると考えられるので、

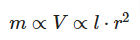
$l\gg r$ と仮定すると、 $\mu\propto S\propto l\cdot r$

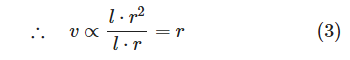
すなわち落下速度は、棒の半径に比例するが棒の長さには依存しない。

⑵ 次に、N N 個の塩基がつらなったDNAの二本鎖が、網目状のゲル中を電界強度 E E のもとで移動する場合を考える（図２（b））。

この場合は、電界からDNAに働く力がなので、電場をかけて十分時間が経った後のDNAの速度 $v$ は次のようになる。

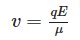
ここで、 $q$ はDNAの持つ電荷であり、 $N$ に比例する。 $\mu$ はDNAとゲルとのあいだの摩擦係数である。

N があまり大きくないとき、DNAは球状に丸まっており $\mu \propto N^{2}$ がなりたつ。

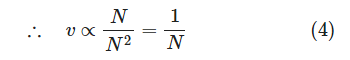
DNAの速度はDNAの長さ $N$ に反比例する。

すなわち、DNAの長さ $N$ の減少関数となり、物体の落下運動の場合の増加関数と逆の依存性を示す。
これは、物体の落下運動の場合は摩擦が物体の表面のみに働くが、DNAの場合は球状に丸まっていても、その内部においてもDNA鎖とゲルの間で摩擦力が働くという違いがあることを反映していると考えられる。

$N$ が大きいとき、DNAは棒状に伸びており、 $\mu \propto N$ が成り立つ。

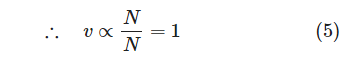
DNAの速度はDNAの長さ $N$ に依存しなくなる。

⑶ 最後に、N N 個の塩基がつらなったDNAの二本鎖が、網目状のゲル中をパルスフィールド電界のもとで移動する場合を考える（図２（c））。

この場合には、パルスフィールド電界のもとでDNAは丸まった状態を保っており、 $\mu \propto N^{2}$ が成り立つ。

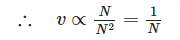
DNAの速度はDNAの長さ $N$ に反比例する。

担当教員プロフィール

1957年熊本県生まれ。
理論物理学から生物物理学、ゲノム科学へと
専門分野を渡り歩いてきました。

教授　西川　哲夫

田舎の実家にあふれていた祖父の大工道具に囲まれて育ち、動く「もの」を作ることが好きで、数学は「もの」の動きを追いかけたり、「もの」を作る際の欠かせない道具だということを次第に意識してきました。田舎の天文少年でありラジオ少年でしたが、名前ばかりで好きになれなかった生物学に実は数学が深く関係していると知り、数理生物学、生物物理学の方面へと足を踏み入れ、今ではヒトゲノム関連の研究が専門です。これまでDNAシーケンサーというDNAの配列情報を読み取る装置の開発を行い、現在はDNA配列に隠された生物の働きについての情報を発見し、データベースにして誰もが利用できるようにしようということが主たるテーマです。
モットーは「なんでもやる」で、「苦手で敬遠してきたこともやってみれば意外と面白いものだ」ということは、私が人生で学んだことの一つです。これまで何をやるに際しても、大学で学んだ物理学の基礎を視点として対象を捉えてきたように思います。高校時代や大学時代は物の見方、視点を醸成する大事な時期だったと思います。

３分でわかる数理工学講座バックナンバー

第１回「スマートフォン市場のシェアを決めるものはなに？」
第２回「雨粒とDNA」
第３回「蛇口から出る水」
第４回「パターンに潜む数理」
第５回「個体間にみられるコミュニケーションと数理工学」
第６回「エネルギーで楽をする話」
第７回「対称性と周期性」
第８回「競争している生物の個体数を予測しよう」
第９回「血管新生」

数学を探せ！ 「雨粒とDNA」