数学を探せ! 「エネルギーで楽をする話」
エネルギーというと皆さんはどんなものを思い浮かべますか。太陽エネルギー等の発電システムでしょうか。もしかしたら、家の大掃除をして「エネルギーを消費した」と言っているかもしれませんね。身の回りのいろいろな現象も、エネルギーを考えるとうまく理解できるものが多いのです。
自然は、可能であればエネルギーをできるだけ使わない状態、低エネルギー状態をとろうとすることが知られています。例えば、針金で作った丸い枠に石鹸で膜を張ってみましょう。水平にして横から見ると、重力で中心部が少し下がっていることに気がつきます。頑張って下がらないように引っ張っているのですが、あのくらいの姿勢が一番楽なのです。
板の両端をもって曲げてみましょう。緩やかなカーブを描いて全体が曲がります。一部分だけが大きく曲がるより、板にとってはそのほうが楽なのです。
これらをエネルギーとして考えてみましょう。ばねは、引っ張ると引っ張られた長さの2乗に比例してエネルギー(弾性エネルギー)が蓄えられます。板が板ばねだと考えると、変形するにつれてどんどんエネルギーが蓄えられていくことになります。このとき全体では一番エネルギー的に低い曲がり方をすることで「楽」な形に変形しようとしているのです。
さて、板を無理に曲げようとすると割れてしまう場合もあります。割れる際のき裂の入り方は様々ですが、なぜそのような割れ方をしたのでしょうか。割れる=切り離されると考えると、我慢しきれないくらい力がかかったために割れてしまうと考えることもできますが、板全体での割れ方を考えると、エネルギー的に低くなるように割れていくと考えることができます。このとき割れるためにエネルギーを必要とするので、シンプルに考えると、全体で
[ 曲げによる(弾性)エネルギー ] + [ 割れるときに使ったエネルギー ]
ができるだけ少なくなるようにき裂が伸びていくととらえることができるのです。その結果、基本的にはできるだけ変形しない形になれるように、そして、できるだけ短い距離で割れるようにき裂は伸びていきます。
ところが、途中に割れづらい場所があったらどうなるでしょうか。その場所を通ろうとすると割れるときにたくさんのエネルギーが必要になるので、できるだけ迂回して割れていこうとします。皆さんもナッツの入ったクッキーなどを割ってみると確認することができます。エネルギー的に「楽」をしようとして割れた結果なのです。

これはどの領域の話か
このようにある関数を最小にするような解を見つける問題は最適化問題の一つとして、広い分野に現れます。特に、関数を引数とした関数(汎関数)の場合には、数学では変分問題として知られており、そこから導出されたオイラー-ラグランジェ方程式は物理学において様々な分野で使われています。これらの問題では、微分(変分)によって極値(停留点)を見つけることで解を探しますが、複雑な式になってしまう場合はコンピュータを使って調べることもあります。
数式を用いた解説
ここでは例として、ひもを使ってエネルギーが最小になるような変形を考えます。両端を固定した、一様な密度を持ったひもが重力で垂れ下がる際には懸垂線という曲線を描きます。
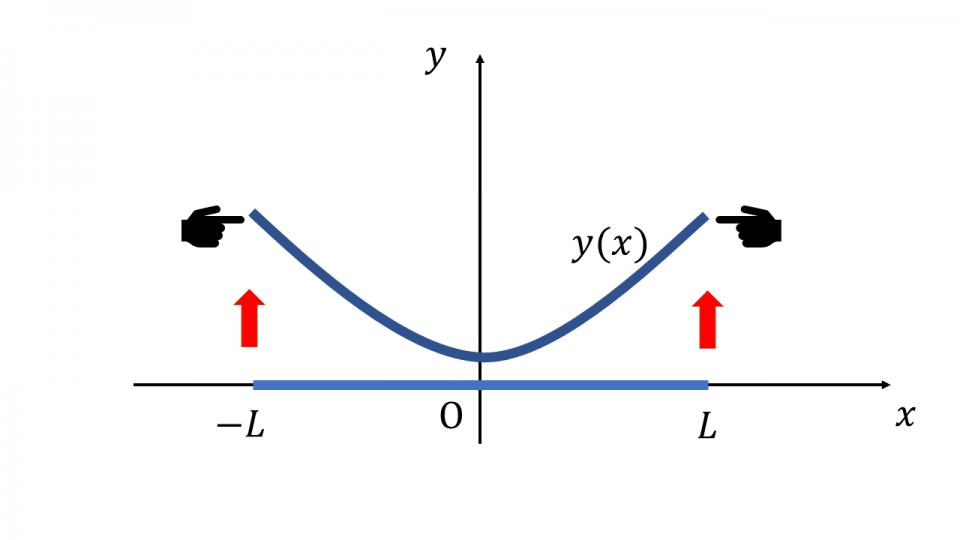
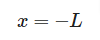
と
が両端になるひもの両端を持って同じ高さに引き上げてみます。密度を
、鉛直上向きのひもの位置を
とすると、エネルギー
は重力加速度 を使って次のように書けます。
このエネルギーを基に、オイラー-ラグランジェ方程式を作ると、
という微分方程式になります。この微分方程式の解を求めるととなり、放物線とは少し違った曲線で垂れ下がっていることがわかります。興味のある人は代入して確かめてみましょう(
:微分した結果をもう1回微分)。

担当教員プロフィール
教授 高石 武史
1962年新潟県生まれ。材料にき裂がどのように生じるか、数理モデルを使って考えていますが、実際の様子を調べるためにはコンピュータでシミュレーションを行います。身の回りで面白いものを見つけたら、すぐに試して結果をグラフやCGにして見ることができるのがコンピュータシミュレーションの楽しいところです。高校までは物理や数学がどちらかというと得意かなという程度だったのですが、大学に入って数式で物理の様々な問題が解けるようになると、いろんなことに興味がわいてきました。研究以外でも、コンピュータとセンサーを使ったアプリを作ったり、簡単な電子工作で IoT 機器を作ったりしています。
3分でわかる数理工学講座バックナンバー
第1回「スマートフォン市場のシェアを決めるものはなに?」
第2回「雨粒とDNA」
第3回「蛇口から出る水」
第4回「パターンに潜む数理」
第5回「個体間にみられるコミュニケーションと数理工学」
第6回「エネルギーで楽をする話」
第7回「対称性と周期性」
第8回「競争している生物の個体数を予測しよう」
第9回「血管新生」

