数理工学センターコラム 「行動を決めるための数理工学」


高校生の皆さんが一週間後に大学の入学試験を控えているとします。残された時間をどの試験科目の勉強に充てるかについて、計画を立てることにしました。各試験科目の勉強時間をどのように決めれば、合格に近づくでしょうか?
入試の当日になりました。自宅から試験会場まで行く際に、電車とバスを乗り継ぐ必要があるとします。複数の移動経路が考えられる場合、どの経路を選んだらよいでしょうか?
このように最適な行動を決めたいという場面は日々の生活で様々にあります。そのような最適な行動を決める際に、数理工学のアプローチを活用できるのです。
数学のどの領域の話か
最適な勉強時間を決めたり、最適な経路を求めるこのような問題は最適化問題と呼ばれています。後に例を挙げますが、こうした問題を数式でうまく表わすことができれば、数学の問題として扱うことができます(これを定式化といいます)。最適化問題を定式化し、問題の解法を示すとともに、問題の性質を明らかにする分野は、最適化理論、あるいは数理計画と呼ばれています。そこでは微積分や線形代数を基礎にして議論が展開され、また、実際に問題を解く際にはコンピュータも活用されています。
数式を用いた解説
ここで、冒頭の勉強時間を決める問題を定式化してみましょう。
入試科目は英語、数学、国語の3科目とします。試験までに15時間の勉強時間を確保できるとし、試験科目の合計得点が最大になるように勉強時間の配分を決めることにします。
定式化にあたって、科目ごとに何時間勉強したら何点がとれるかという勉強時間と得点の関係を把握しておく必要があります。
ここでは、勉強時間と得点の関係に
- 勉強時間が多いほど得点は増える
- 得点の増え方は、それまでの勉強時間が多いほど少なくなる
という特徴があると想定し、勉強時間と得点の関係が図2で表される関数で与えられているとします。数式で表現すると、英語・数学・国語の勉強時間を順にs,t,uとして
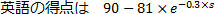
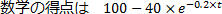
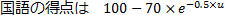
としました(現実にはこの関数を定めることは容易ではないと思われますが、ここでは関数がわかっているとします)。
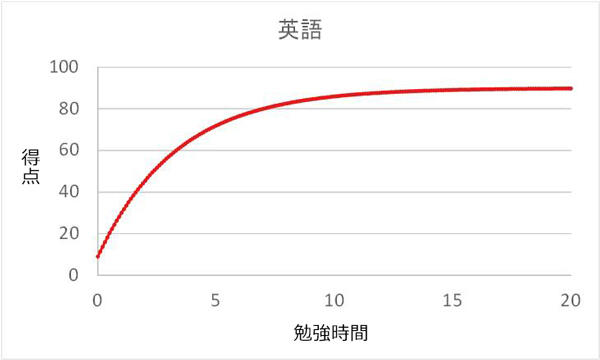
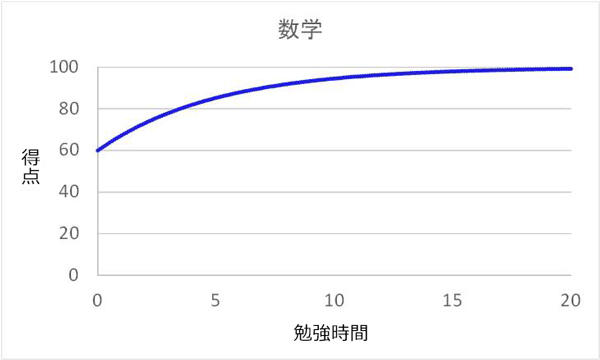
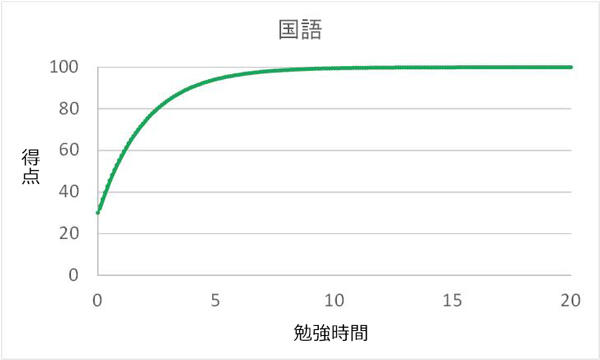
図1:各科目の勉強時間と得点の関係
以上の状況をまとめると、最適な勉強時間を決める問題は次の最適化問題として定式化できます。
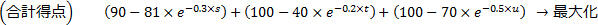
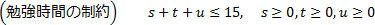
以上のように「最適な行動を決めたい」という問題が定式化されれば、数学の問題として扱うことができるようになります。
最適化問題は社会の中で多く応用されています。企業の生産活動において製品の最適な生産量を決める問題も最適化問題の一種です。これは生産計画問題と呼ばれています。また、株や債券などへの投資の際に投資額の配分を決める問題はポートフォリオ最適化問題と呼ばれています。
このように、数理工学的なアプローチで社会の課題を解決する場面は数多いのです。


参考文献
- 新版 数理計画入門、福島雅夫著、朝倉書店(2011)

著者
山中 卓
1983年茨城県生まれ。高校生のころを振り返ると、数学の分野の中では特に確率に興味をもっていました。サイコロ投げや天気予報などの不確実な事柄を扱うことができることに面白さを感じていたのだと思います。今では金融分野の課題を数理工学の立場から解決することを目指して研究活動を行っています。
※この講座の著作権は著者にあります。無断引用や転載等はお断りいたします。

