数理工学センターコラム 「バクテリアが見せるインテリジェンス」

バクテリアと聞いて、どんなイメージが思い浮かびますか?
バクテリアは私たちの周りのどこにでもいる、日常的に共存している生き物です。食中毒の原因になるブドウ球菌を知っていると怖いイメージがあるかもしれませんが、私たちが普段食べているチーズや納豆、ヨーグルトなどは、その発酵過程においてバクテリアが重要な役割を果たしています。
このようなバクテリアが、実は私たちの想像を超えて、かなり頭が良い微生物であることを紹介しましょう。

ここで扱うバクテリアは、納豆菌と同じ仲間の極めて安全性が高い枯草菌(こそうきん)です。 枯草菌(以後、バクテリアと呼びます)は、細長い糸状の鞭毛(べんもう)を回転させることから、水中で動き回ることができますが、特に養分がある環境では、成長と細胞分裂を繰り返してどんどん数が増えていき、やがてコロニーと呼ばれる菌のかたまりを形成します。
ここではシャーレーの中に一定濃度の養分を含んだ寒天を入れ、その中央にバクテリアを1点接種した寒天培養実験を考えましょう。バクテリアにとって養分濃度と寒天密度(高いと動きやすく、低いと動きにくい)は重要な環境条件であり、それらが変化するとき、それらに応じて様々なコロニーを形成することが知られています[1]。極端な例では、養分濃度が高く、寒天密度が低い(運動性が高い、つまり、動きやすい)という良い環境条件では、コロニーはディスク形状(円形状)で一様に拡がっていきますが、環境が劣悪な条件になると、状況が一変します。彼等は、図1のように、コロニーと養分領域の境界の長さができるだけ長くなるように、非常に複雑な形状を取りながらゆっくりとコロニーを形成するのです。このとき驚くことに、境界の長さは円形状に比べて何十倍も長いのです。つまり、バクテリアは環境条件が悪くなると、わずかな養分を有効に取り入れるために境界の長さをできるだけ長くしているといえるのです。
以上のように、バクテリアは環境の変化に対応して生き残るためにコロニーの形状を変えるというインテリジェンスを身に付けているのです。
この背後にある数学
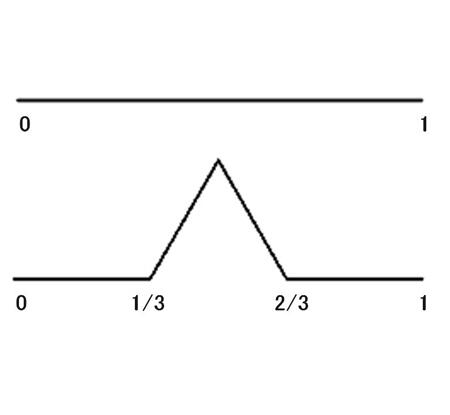
バクテリアが作り出す複雑な形状の仕組みを理解するためには、「2点間をつなぐ曲線の長さを可能な限り長くする曲線はどのようなものか?」という問題が考えられています。この問題はすでに1904年、スエーデンの数学者コッホによって次のように答えられています。
長さ1の線分を3等分し、分割した2点を頂点とする正3角形を図2のように作ります。このとき、得られる図形の線分の長さは4/3 = 1.33…となります。これを4回繰り返すと、その長さは (4/3)4 = 3.16…。更に、続けて50回行うと、(4/3)50 = 1,765,780.96…となり、何と曲線の長さは元の長さのほぼ170万倍になることがわかります。
ここで使われている結果は数学と呼べるほどもない、簡単なものですが、コッホは当然ながらバクテリアコロニーなどに興味はなく、数学への興味から、純数学的に考えたものです。これが数学の面白いところであり、今では生物、物理など自然科学の様々な分野に現れる複雑な形状を理解するために役立っているのです。
参考文献
[1] 松下貢、三村昌泰:バクテリアコロニーの多様性(生物にみられるパターンとその起源(編:松下貢))、東大出版会 (2005)

著者
三村 昌泰
現在、私の専門分野は現象数理学である。これを一言で説明すると、これまで発展してきた数学やコンピューターを道具として用いて現象の解明を行うことを目的とする、そしてその道具がまだ不完全であれば、それを開発していこうという分野である。なぜ私がこのような学問分野に到ったかは、中学生の頃数学の先生から、今では地球の大きさは正確にわかっているが、紀元前3世紀ごろすでに地球が丸く、大きさもわかっていたとのことで、それには当時知られていた相似則という単純な数学が使われていたことを知ったことである。この時から、「数学は役に立つ」ということに驚くとともに、「役に立つ数学」を学びたいと思ってこれまでやってきたのである。
※この講座の著作権は著者にあります。無断引用や転載等はお断りいたします。

