数理工学センターコラム 「The Monty Hall problem: To switch or not!」
Introduction
The Monty Hall problem is about the chance of a winning a game show. It is based on the television show, Let’s make a Deal, hosted by Monty Hall. It is a very famous and amusing problem in Mathematics.
In the game show, there are three doors: A, B and C. There is a brand-new expensive car behind one door and jokers behind other two doors. There is one player and one host. Nobody except the host knows what is behind each door. The game starts with the player choosing one door but does not open it yet. After that, host open a door different from the door chosen by the player to show that it has a joker behind it. At this moment, there are two closed doors and one open door with the joker behind it. One of the two closed doors has a car behind it but the player does not know which one is it. The rule of the game is that the host shows a door with the joker behind it and offer the player to let him switch between his original chosen door and the remaining closed door. The question is whether the player should switch doors to increase his chance of winning or not?
You must have studied that to calculate the chance of an event, it is the number of favorable outcomes by the total number of outcomes. For example, the chance of getting a head when tossing a coin is 1/2. At the start of the game, when there were three closed doors, the probability of winning the car is 1/3, that is 0.33 chance. However, when the host opens a door with the joker, what is the probability of winning the car? Many people think that both doors have equal chance of having a car behind it. That is, the probability of winning a car when there are two closed doors is 1/2. This means that the player has 50/50 chance of winning the car and so, it does not matter if he switches or stays with his originally chosen door. However, this is not true! This is a problem of statistical illusion. Using the conditional probability, we can show that the probability of winning is greater if the player switches his decision. The mathematical argument is given below.
What area of Mathematics?
The Monty Hall game is a game of chance and uses the basics of Probability theory (確率). Probability is a very important branch of mathematics which is used in statistics, finance, insurance, and markets. We use probability in everyday life without realizing it. It is used in the weather forecast, or in medical studies where we calculate the probability that the person has flu or not, based on the positive test results. Such probabilities of an occurrence of an event given the another related event has occurred are called “conditional probability”. The conditional probability is calculated using the Bayes’ Theorem. It is also used in many puzzles and games. Based on the certain situations or conditions that have already occurred, we try to get the likelihood of an event occurrence. The Bayes’ theorem and conditional probability are fundamental to Probability and everyday life. In the University, we study sample spaces, random variables, probability distributions, law of large numbers and central limit theorems. To study and understand these topics, Bayes’ theorem and conditional probability are very important. Bayes’ theorem is as important to the field of Probability as is the Pythagorean theorem to the field of Geometry. If you are interested, please look up ベイズの定理. We can calculate the conditional probability for events X and Y using the following formula:
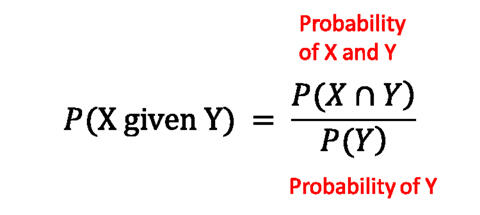
A mathematical explanation
Let us find the answer to the game. What is your answer? Should the player change the door or not? Many people would say to stay and not change. But by using the conditional probability, we will show that it is best to switch the door every time to increase the chance of winning.
There are three situations: car is either behind door A, B or C. Let’s say car is behind the door B and doors A, C have jokers behind it. The game starts, the player can choose any door. If he chooses door A then the host has to open door C. Using the above formula of conditional probability, the probability of winning by switching, given that the player chose door A and host opened door C is equal to the probability of car behind door B and host opening door C divided by the probability of host opening door C.
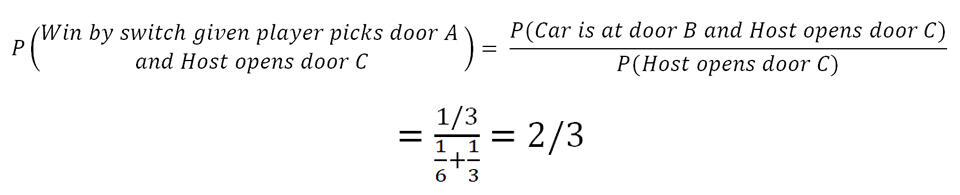
So, the conditional probability of winning by switching is 2/3. In simpler terms, if the player switches the door then he has the chance of winning a car two times out of three.
The probability of every possible outcome given that the player chooses door A, door B or door C is presented in the following diagram.
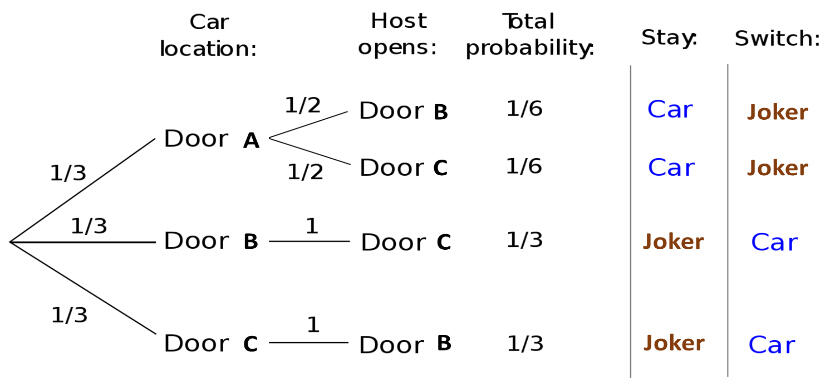
A simpler explanation of the chance of winning the car is explained below:
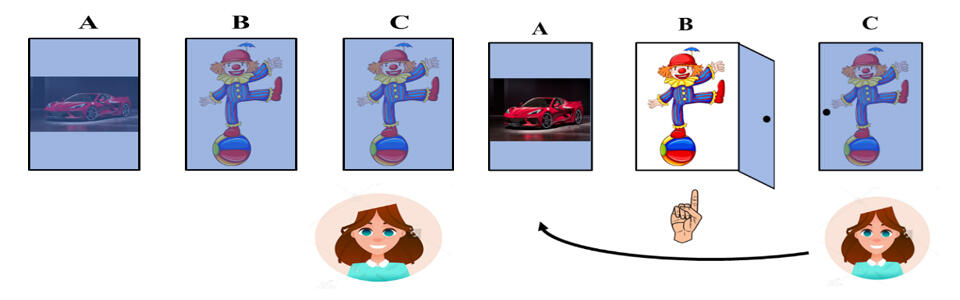
- Player picks door A and door A has a car behind it.
In this case, the host will either open door B or C to show the joker. If the player switches, then he will lose the car prize.
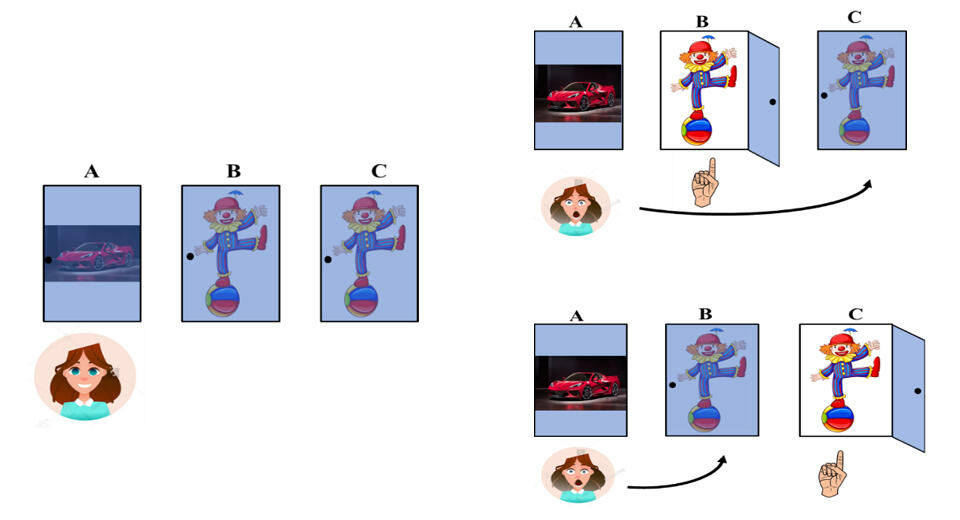
- Player picks door B and door A has a car behind it.
In this case, the host has to open the door C as only door C has the joker and he cannot show the door A with the car. So, if the player switches to door A then he wins the car prize.
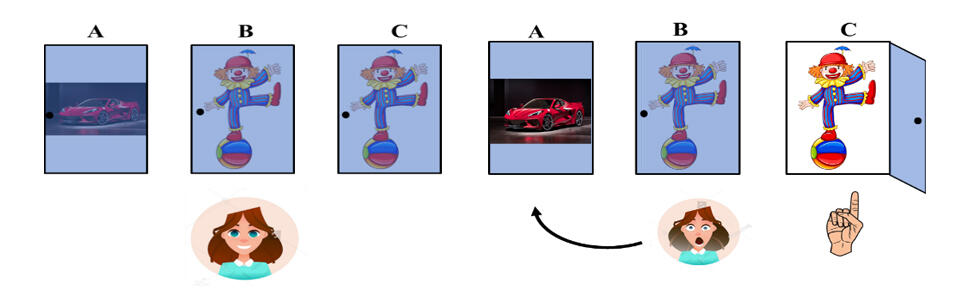
- Player picks door C and door A has a car behind it.
IThis case is same as the above case. In this case, the host has to open the door B as only door B has the joker and he cannot show the door A with the car. So, if the player switches to door A then he wins the car prize.
We can see from the above illustration that the player wins two times out of three if he switches the door. What about the cases when the door B has a car or door C has a car behind it? The similar argument can be applied.
What if there are more than three doors? The problem becomes more interesting. Suppose, there are four doors: A, B, C and D. Only one has a car and other three has jokers behind it but you do not know it! I ask you to choose a door. Are you done? I open a door to show a joker and ask you “Do you want to stay or switch?” What is your answer? Read about the Bayes’ theorem and conditional probability and try to find the answer!
Authors
Sushma Kumari
Hi! I was born in India and finished my Masters in Mathematics from IITH in India. I came to Japan in 2015 to pursue Ph.D. from the Kyoto University. When I was a child, I used to do a lot of calculations at home. I like mathematics a lot and I used to wonder how the news reporter could say that tomorrow it is going to rain or there is a possibility of thunderstorm in the coming week. What is the chance of winning a lottery? How are players lined up in a baseball game based on their batting’s average and how is it calculated? All these can be understood using the probability theory and so, I chose to study probability at the university. My current research on statistical machine learning is based on the theory of probability and statistics. Almost every field applies some part of probability, so I advise you to understand basic probability to have a strong career.
※この講座の著作権は著者にあります。無断引用や転載等はお断りいたします。

